1. $70^{\circ}$角的余角是
20
$^{\circ}$,补角是110
$^{\circ}$;一个角的补角等于$125^{\circ}$,那么这个角等于55
$^{\circ}$。答案:20;110;55
2. 一个锐角等于$m^{\circ}$,则它的余角等于
(90 - m)
$^{\circ}$,它的补角等于(180 - m)
$^{\circ}$,它的余角比它的补角小90
$^{\circ}$。答案:(90 - m);(180 - m);90
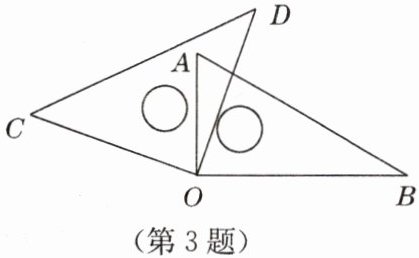
3. 将一副直角三角尺按如图所示放置,若$\angle BOC = 160^{\circ}$,则$\angle AOD$的大小为(
A.$15^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$30^{\circ}$
B
)
A.$15^{\circ}$
B.$20^{\circ}$
C.$25^{\circ}$
D.$30^{\circ}$
答案:B
解析:
由题意知,一副直角三角尺的直角顶点重合于点O,所以∠AOB=90°,∠COD=90°。
因为∠AOB + ∠COD = ∠AOD + ∠DOB + ∠COD,而∠DOB + ∠COD = ∠BOC,所以∠AOB + ∠COD = ∠AOD + ∠BOC。
已知∠BOC=160°,则∠AOD = ∠AOB + ∠COD - ∠BOC = 90° + 90° - 160° = 20°。
B
因为∠AOB + ∠COD = ∠AOD + ∠DOB + ∠COD,而∠DOB + ∠COD = ∠BOC,所以∠AOB + ∠COD = ∠AOD + ∠BOC。
已知∠BOC=160°,则∠AOD = ∠AOB + ∠COD - ∠BOC = 90° + 90° - 160° = 20°。
B
4. 如果$\angle \alpha和\angle \beta$互补,且$\angle \alpha > \angle \beta$,则下列表示$\angle \beta$的余角的式子中:①$90^{\circ} - \angle \beta$;②$\angle \alpha - 90^{\circ}$;③$\frac{1}{2}(\angle \alpha + \angle \beta)$;④$\frac{1}{2}(\angle \alpha - \angle \beta)$。其中不正确的是(
A.①
B.②
C.③
D.④
C
)A.①
B.②
C.③
D.④
答案:C
解析:
因为$\angle\alpha$和$\angle\beta$互补,所以$\angle\alpha+\angle\beta=180^{\circ}$。
$\angle\beta$的余角为$90^{\circ}-\angle\beta$,故①正确。
由$\angle\alpha+\angle\beta=180^{\circ}$得$\angle\alpha=180^{\circ}-\angle\beta$,则$\angle\alpha - 90^{\circ}=180^{\circ}-\angle\beta - 90^{\circ}=90^{\circ}-\angle\beta$,故②正确。
$\frac{1}{2}(\angle\alpha+\angle\beta)=\frac{1}{2}×180^{\circ}=90^{\circ}$,不是$\angle\beta$的余角,故③不正确。
$\frac{1}{2}(\angle\alpha - \angle\beta)=\frac{1}{2}(180^{\circ}-\angle\beta - \angle\beta)=90^{\circ}-\angle\beta$,故④正确。
C
$\angle\beta$的余角为$90^{\circ}-\angle\beta$,故①正确。
由$\angle\alpha+\angle\beta=180^{\circ}$得$\angle\alpha=180^{\circ}-\angle\beta$,则$\angle\alpha - 90^{\circ}=180^{\circ}-\angle\beta - 90^{\circ}=90^{\circ}-\angle\beta$,故②正确。
$\frac{1}{2}(\angle\alpha+\angle\beta)=\frac{1}{2}×180^{\circ}=90^{\circ}$,不是$\angle\beta$的余角,故③不正确。
$\frac{1}{2}(\angle\alpha - \angle\beta)=\frac{1}{2}(180^{\circ}-\angle\beta - \angle\beta)=90^{\circ}-\angle\beta$,故④正确。
C
5. 如果$\angle A与它的余角之比为1:2$,$\angle B与\angle A$互为补角,求$\angle B$的度数。
答案:150°
解析:
设$\angle A$的度数为$x$,则它的余角为$90° - x$。
因为$\angle A$与它的余角之比为$1:2$,所以$x:(90° - x)=1:2$,即$2x = 90° - x$,解得$3x=90°$,$x = 30°$。
因为$\angle B$与$\angle A$互为补角,所以$\angle B=180° - \angle A=180° - 30°=150°$。
$150°$
因为$\angle A$与它的余角之比为$1:2$,所以$x:(90° - x)=1:2$,即$2x = 90° - x$,解得$3x=90°$,$x = 30°$。
因为$\angle B$与$\angle A$互为补角,所以$\angle B=180° - \angle A=180° - 30°=150°$。
$150°$
6. 一个角的补角是它的余角的$4$倍,求这个角的补角和这个角的余角的度数。
答案:120°,30°
解析:
设这个角的度数为$x$。
由题意得:$180° - x = 4(90° - x)$
解得:$x = 60°$
这个角的补角的度数为:$180° - 60° = 120°$
这个角的余角的度数为:$90° - 60° = 30°$
120°,30°
由题意得:$180° - x = 4(90° - x)$
解得:$x = 60°$
这个角的补角的度数为:$180° - 60° = 120°$
这个角的余角的度数为:$90° - 60° = 30°$
120°,30°