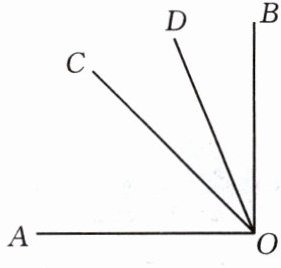
问题 如图,$\angle AOD与\angle BOD$互余,$\angle AOD比\angle BOD大46^{\circ}$,$OC平分\angle AOB$,求$\angle COD$的度数。
名师指导
设$\angle BOD为x^{\circ}$,则$\angle AOD为(46 + x)^{\circ}$,根据$\angle AOD与\angle BOD互余得到\angle AOB = 90^{\circ}$,则$x+(46 + x)= 90$,再根据$OC平分\angle AOB$,求出$\angle BOC$。
解题示范(学生在教师指导下,独立完成)
解:
名师指导
设$\angle BOD为x^{\circ}$,则$\angle AOD为(46 + x)^{\circ}$,根据$\angle AOD与\angle BOD互余得到\angle AOB = 90^{\circ}$,则$x+(46 + x)= 90$,再根据$OC平分\angle AOB$,求出$\angle BOC$。
解题示范(学生在教师指导下,独立完成)
解:

答案:解:
设$\angle BOD = x^{\circ}$,则$\angle AOD = (x + 46)^{\circ}$。
因为$\angle AOD$与$\angle BOD$互余,
所以$\angle AOD + \angle BOD = 90^{\circ}$,
即$x + (x + 46) = 90$,
$2x + 46 = 90$,
$2x = 44$,
$x = 22$。
所以$\angle BOD = 22^{\circ}$,$\angle AOD = 22^{\circ} + 46^{\circ} = 68^{\circ}$。
则$\angle AOB =\angle AOD + \angle BOD= 90^{\circ}$。
因为$OC$平分$\angle AOB$,
所以$\angle BOC = \frac{1}{2}\angle AOB = 45^{\circ}$。
所以$\angle COD = \angle BOC - \angle BOD = 45^{\circ} - 22^{\circ} = 23^{\circ}$。
综上,$\angle COD$的度数为$23^{\circ}$。
设$\angle BOD = x^{\circ}$,则$\angle AOD = (x + 46)^{\circ}$。
因为$\angle AOD$与$\angle BOD$互余,
所以$\angle AOD + \angle BOD = 90^{\circ}$,
即$x + (x + 46) = 90$,
$2x + 46 = 90$,
$2x = 44$,
$x = 22$。
所以$\angle BOD = 22^{\circ}$,$\angle AOD = 22^{\circ} + 46^{\circ} = 68^{\circ}$。
则$\angle AOB =\angle AOD + \angle BOD= 90^{\circ}$。
因为$OC$平分$\angle AOB$,
所以$\angle BOC = \frac{1}{2}\angle AOB = 45^{\circ}$。
所以$\angle COD = \angle BOC - \angle BOD = 45^{\circ} - 22^{\circ} = 23^{\circ}$。
综上,$\angle COD$的度数为$23^{\circ}$。
1. 如图,点$A$,$O$,$B$在同一条直线上,$\angle AOC = \angle BOC$,若$\angle 1 = \angle 2$,则图中与$\angle 2$互余的角共有(

A.$2$个
B.$3$个
C.$4$个
D.$5$个
A
)
A.$2$个
B.$3$个
C.$4$个
D.$5$个
答案:A
解析:
∵点A,O,B在同一条直线上,∠AOC=∠BOC,
∴∠AOC=∠BOC=90°.
∵∠1=∠2,∠1+∠AOE=∠AOC=90°,
∴∠2+∠AOE=90°,即∠AOE与∠2互余.
∵∠2+∠COD=∠BOC=90°,
∴∠COD与∠2互余.
综上,与∠2互余的角共有2个.
A
2. 设$\angle \alpha$,$\angle \beta的度数分别为(2n + 5)^{\circ}和(65 - n)^{\circ}$,且$\angle \alpha$,$\angle \beta都是\angle \gamma$的补角。
(1)求$n$的值;(2)$\angle \alpha与\angle \beta$能否互余,请说明理由。
(1)求$n$的值;(2)$\angle \alpha与\angle \beta$能否互余,请说明理由。
答案:(1)n = 20;(2)∠α与∠β互余,理由如下:∠α=(2n + 5)° = 45°,∠β=(65 - n)° = 45°.
∵∠α + ∠β = 90°,
∴∠α与∠β互为余角.
∵∠α + ∠β = 90°,
∴∠α与∠β互为余角.
3. $\angle 1与\angle 2$互补,$\angle 1 - \angle 2 = 40^{\circ}$,求$\angle 1与\angle 2$的度数。
答案:∠1 = 110°;∠2 = 70°
解析:
解:因为∠1与∠2互补,所以∠1+∠2=180°。
又因为∠1-∠2=40°,联立可得:
∠1=(180°+40°)÷2=110°
∠2=180°-∠1=180°-110°=70°
∠1=110°;∠2=70°
又因为∠1-∠2=40°,联立可得:
∠1=(180°+40°)÷2=110°
∠2=180°-∠1=180°-110°=70°
∠1=110°;∠2=70°
4. 如图,点$A$,$O$,$B$在一条直线上,$\angle AOC比\angle BOC大100^{\circ}$,$\angle BOC与\angle BOD$互余,$OE平分\angle AOC$,求$\angle DOE$的度数。


答案:160°
解析:
设$\angle BOC = x$,则$\angle AOC = x + 100°$。
因为点$A$,$O$,$B$在一条直线上,所以$\angle AOC+\angle BOC=180°$,即$x + 100°+x=180°$,解得$x = 40°$,故$\angle BOC = 40°$,$\angle AOC=140°$。
因为$\angle BOC$与$\angle BOD$互余,所以$\angle BOD = 90°-\angle BOC=90° - 40°=50°$。
因为$OE$平分$\angle AOC$,所以$\angle AOE=\frac{1}{2}\angle AOC=\frac{1}{2}×140° = 70°$。
$\angle AOD=180°-\angle BOD=180° - 50°=130°$。
$\angle DOE=\angle AOD-\angle AOE=130° - 70°=60°$。
$60°$
因为点$A$,$O$,$B$在一条直线上,所以$\angle AOC+\angle BOC=180°$,即$x + 100°+x=180°$,解得$x = 40°$,故$\angle BOC = 40°$,$\angle AOC=140°$。
因为$\angle BOC$与$\angle BOD$互余,所以$\angle BOD = 90°-\angle BOC=90° - 40°=50°$。
因为$OE$平分$\angle AOC$,所以$\angle AOE=\frac{1}{2}\angle AOC=\frac{1}{2}×140° = 70°$。
$\angle AOD=180°-\angle BOD=180° - 50°=130°$。
$\angle DOE=\angle AOD-\angle AOE=130° - 70°=60°$。
$60°$