1. 计算$(-4)×(-\frac{1}{2})$的结果是(
A.$-2$
B.2
C.$-8$
D.8
B
)A.$-2$
B.2
C.$-8$
D.8
答案:B
解析:
$(-4)×(-\frac{1}{2})=4×\frac{1}{2}=2$,结果为2,选B。
2. 数轴上的三点$A$,$B$,$C所表示的数分别为a$,$b$,$c且满足a + b>0$,$ac < 0$,则原点在(
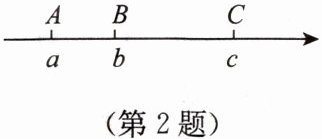
A.点$A$左侧
B.点$A与点B$之间(不含点$A$、点$B$)
C.点$B与点C$之间(不含点$B$、点$C$)
D.点$C$右侧
B
)
A.点$A$左侧
B.点$A与点B$之间(不含点$A$、点$B$)
C.点$B与点C$之间(不含点$B$、点$C$)
D.点$C$右侧
答案:B
解析:
由数轴知$a < b < c$。
因为$ac < 0$,所以$a$、$c$异号,即$a < 0$,$c > 0$。
因为$a + b > 0$,所以$b > -a$,又$a < 0$,则$-a > 0$,故$b > 0$。
综上,$a < 0 < b < c$,原点在点$A$与点$B$之间。
B
因为$ac < 0$,所以$a$、$c$异号,即$a < 0$,$c > 0$。
因为$a + b > 0$,所以$b > -a$,又$a < 0$,则$-a > 0$,故$b > 0$。
综上,$a < 0 < b < c$,原点在点$A$与点$B$之间。
B
3. 数$a$,$b$,$c$表示的点在数轴上的位置如图所示,则下列结论正确的是(

A.$abc>0$
B.$a(b - c)>0$
C.$(a + b)c>0$
D.$(a - c)b>0$
B
)
A.$abc>0$
B.$a(b - c)>0$
C.$(a + b)c>0$
D.$(a - c)b>0$
答案:B
解析:
由数轴可知:$a < -2$,$0 < b < 1$,$c > 1$。
A. $a < 0$,$b > 0$,$c > 0$,则$abc < 0$,A错误。
B. $b - c < 0$,$a < 0$,则$a(b - c) > 0$,B正确。
C. $a + b < 0$,$c > 0$,则$(a + b)c < 0$,C错误。
D. $a - c < 0$,$b > 0$,则$(a - c)b < 0$,D错误。
B
A. $a < 0$,$b > 0$,$c > 0$,则$abc < 0$,A错误。
B. $b - c < 0$,$a < 0$,则$a(b - c) > 0$,B正确。
C. $a + b < 0$,$c > 0$,则$(a + b)c < 0$,C错误。
D. $a - c < 0$,$b > 0$,则$(a - c)b < 0$,D错误。
B
4. 在数5,$-3$,2,$-6$中任取两个数相乘,其中积最大的是(
A.$-30$
B.10
C.$-15$
D.18
D
)A.$-30$
B.10
C.$-15$
D.18
答案:D
解析:
在数5,-3,2,-6中任取两个数相乘,所有可能的积为:
$5×(-3)=-15$
$5×2=10$
$5×(-6)=-30$
$(-3)×2=-6$
$(-3)×(-6)=18$
$2×(-6)=-12$
比较这些积的大小:$18>10>-6>-12>-15>-30$,其中最大的积是18。
D
$5×(-3)=-15$
$5×2=10$
$5×(-6)=-30$
$(-3)×2=-6$
$(-3)×(-6)=18$
$2×(-6)=-12$
比较这些积的大小:$18>10>-6>-12>-15>-30$,其中最大的积是18。
D
5. 计算:
(1) $(-8.125)×(-8)$; (2) $(+20\frac{1}{4})×(-20\frac{4}{9})$;
(3) $-\vert -1\vert ×(-0.8)$; (4) $-\vert -2\vert ×(1 - 2)$.
(1) $(-8.125)×(-8)$; (2) $(+20\frac{1}{4})×(-20\frac{4}{9})$;
(3) $-\vert -1\vert ×(-0.8)$; (4) $-\vert -2\vert ×(1 - 2)$.
答案:(1)65;(2)-414;(3)0.8;(4)2.
解析:
(1) $(-8.125)×(-8)$
$=8.125×8$
$=65$
(2) $(+20\frac{1}{4})×(-20\frac{4}{9})$
$=-\left(20+\frac{1}{4}\right)\left(20+\frac{4}{9}\right)$
$=-\left(20×20 + 20×\frac{4}{9}+\frac{1}{4}×20+\frac{1}{4}×\frac{4}{9}\right)$
$=-\left(400+\frac{80}{9}+5+\frac{1}{9}\right)$
$=-\left(405 + 9\right)$
$=-414$
(3) $-\vert -1\vert ×(-0.8)$
$=-1×(-0.8)$
$=0.8$
(4) $-\vert -2\vert ×(1 - 2)$
$=-2×(-1)$
$=2$
计算:
$(\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2026})×(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2025})-(\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2025})×(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2026})$.
$(\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2026})×(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2025})-(\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2025})×(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2026})$.
答案:设$x=\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{2025}$,则原式$=(x+\frac{1}{2026})×(1+x)-x(1+\frac{1}{2026}+x)=x+x^{2}+\frac{1}{2026}+\frac{x}{2026}-x-\frac{x}{2026}-x^{2}=\frac{1}{2026}$.