1. 比 4 的相反数小 3 的数是(
A.$-7$
B.7
C.$\pm 7$
D.0
A
)A.$-7$
B.7
C.$\pm 7$
D.0
答案:A
解析:
4的相反数是$-4$,比$-4$小3的数是$-4 - 3 = -7$。A
2. 丁丁做了 4 道题:①$(-1)^{2026}= -1$;②$0-(-1)= -1$;③$-\frac{1}{2}+\frac{1}{3}= -\frac{1}{6}$;④$\frac{1}{2}÷ (-2)= -1$. 请你帮他检查一下,他一共做对了(
A.1 题
B.2 题
C.3 题
D.4 题
A
)A.1 题
B.2 题
C.3 题
D.4 题
答案:A
解析:
①$(-1)^{2026}=1$,错误;
②$0-(-1)=0+1=1$,错误;
③$-\frac{1}{2}+\frac{1}{3}=-\frac{3}{6}+\frac{2}{6}=-\frac{1}{6}$,正确;
④$\frac{1}{2}÷(-2)=\frac{1}{2}×(-\frac{1}{2})=-\frac{1}{4}$,错误。
做对1题。
A
②$0-(-1)=0+1=1$,错误;
③$-\frac{1}{2}+\frac{1}{3}=-\frac{3}{6}+\frac{2}{6}=-\frac{1}{6}$,正确;
④$\frac{1}{2}÷(-2)=\frac{1}{2}×(-\frac{1}{2})=-\frac{1}{4}$,错误。
做对1题。
A
3. 如果$a<0$,$b<0$,且$|a|>|b|$,那么$a+(-b)$的值一定是(
A.正数
B.负数
C.0
D.无法确定
B
)A.正数
B.负数
C.0
D.无法确定
答案:B
解析:
因为$a < 0$,$b < 0$,所以$-b > 0$。又因为$|a| > |b|$,即$|a| > |-b|$,一个负数的绝对值大于一个正数的绝对值,它们相加的结果为负数,所以$a + (-b)$的值一定是负数。
B
B
4. 如果一个数的平方与这个数的差等于 0,那么这个数只能是(
A.0
B.1
C.1 或$-1$
D.0 或 1
D
)A.0
B.1
C.1 或$-1$
D.0 或 1
答案:D
解析:
设这个数为$x$,由题意得$x^2 - x = 0$,即$x(x - 1) = 0$,解得$x = 0$或$x = 1$。
D
D
5. 若$x$是 3 的相反数,$|y|= 4$,则$x-y$的值是(
A.$-7$
B.1
C.$-1$或 7
D.1 或$-7$
D
)A.$-7$
B.1
C.$-1$或 7
D.1 或$-7$
答案:D
解析:
因为$x$是$3$的相反数,所以$x=-3$。
因为$|y| = 4$,所以$y = 4$或$y=-4$。
当$y = 4$时,$x-y=-3 - 4=-7$;
当$y=-4$时,$x-y=-3-(-4)=1$。
综上,$x - y$的值是$1$或$-7$。
D
因为$|y| = 4$,所以$y = 4$或$y=-4$。
当$y = 4$时,$x-y=-3 - 4=-7$;
当$y=-4$时,$x-y=-3-(-4)=1$。
综上,$x - y$的值是$1$或$-7$。
D
6. $(-2)^{11}+(-2)^{10}$的值是(
A.$-2$
B.$(-2)^{21}$
C.0
D.$-2^{10}$
D
)A.$-2$
B.$(-2)^{21}$
C.0
D.$-2^{10}$
答案:D
解析:
$(-2)^{11}+(-2)^{10}$
$=(-2)^{10}×(-2)+(-2)^{10}×1$
$=(-2)^{10}×(-2 + 1)$
$=(-2)^{10}×(-1)$
$=2^{10}×(-1)$
$=-2^{10}$
D
$=(-2)^{10}×(-2)+(-2)^{10}×1$
$=(-2)^{10}×(-2 + 1)$
$=(-2)^{10}×(-1)$
$=2^{10}×(-1)$
$=-2^{10}$
D
7. $(-2)^{11}-(-2)^{10}$的值是(
A.$-2$
B.$(-2)^{21}$
C.$-3× 2^{10}$
D.$-2^{10}$
C
)A.$-2$
B.$(-2)^{21}$
C.$-3× 2^{10}$
D.$-2^{10}$
答案:C
解析:
$(-2)^{11}-(-2)^{10}$
$=(-2)^{10}×(-2)-(-2)^{10}×1$
$=(-2)^{10}×(-2 - 1)$
$=2^{10}×(-3)$
$=-3×2^{10}$
C
$=(-2)^{10}×(-2)-(-2)^{10}×1$
$=(-2)^{10}×(-2 - 1)$
$=2^{10}×(-3)$
$=-3×2^{10}$
C
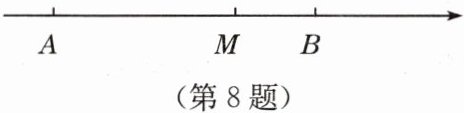
8. 如图,数轴上点$A$,$M$,$B分别表示数a$,$a+b$,$b$,那么下列运算结果一定是正数的是(
A.$ab$
B.$a-b$
C.$a+b$
D.$|a|-b$
C
)
A.$ab$
B.$a-b$
C.$a+b$
D.$|a|-b$
答案:C
解析:
由数轴可知:$a < a+b < b$。
由$a < a+b$得:$b > 0$;
由$a+b < b$得:$a < 0$;
由$a < b$且$a < 0$,$b > 0$,无法确定$|a|$与$b$的大小。
A.$ab$:$a < 0$,$b > 0$,则$ab < 0$;
B.$a - b$:$a < 0$,$b > 0$,则$a - b < 0$;
C.$a + b$:由数轴知$a + b$在原点右侧,$a + b > 0$;
D.$|a| - b$:无法确定$|a|$与$b$的大小,结果不一定为正。
C
由$a < a+b$得:$b > 0$;
由$a+b < b$得:$a < 0$;
由$a < b$且$a < 0$,$b > 0$,无法确定$|a|$与$b$的大小。
A.$ab$:$a < 0$,$b > 0$,则$ab < 0$;
B.$a - b$:$a < 0$,$b > 0$,则$a - b < 0$;
C.$a + b$:由数轴知$a + b$在原点右侧,$a + b > 0$;
D.$|a| - b$:无法确定$|a|$与$b$的大小,结果不一定为正。
C
9. 如图,数轴上点$A$的初始位置表示的数为 1. 现点$A$做如下移动:第 1 次点$A$向左移动 3 个单位长度至点$A_1$,第 2 次从点$A_1$向右移动 6 个单位长度至点$A_2$,第 3 次从点$A_2$向左移动 9 个单位长度至点$A_3$……按照这种移动方式进行下去,如果点$A_n$与原点的距离不小于 20,那么$n$的最小值是(

A.12
B.13
C.14
D.15
B
)
A.12
B.13
C.14
D.15
答案:B
解析:
点A初始位置表示的数为1。
第1次移动:$1 - 3 = -2$,点$A_1$表示$-2$,与原点距离$2$;
第2次移动:$-2 + 6 = 4$,点$A_2$表示$4$,与原点距离$4$;
第3次移动:$4 - 9 = -5$,点$A_3$表示$-5$,与原点距离$5$;
第4次移动:$-5 + 12 = 7$,点$A_4$表示$7$,与原点距离$7$;
第5次移动:$7 - 15 = -8$,点$A_5$表示$-8$,与原点距离$8$;
第6次移动:$-8 + 18 = 10$,点$A_6$表示$10$,与原点距离$10$;
第7次移动:$10 - 21 = -11$,点$A_7$表示$-11$,与原点距离$11$;
第8次移动:$-11 + 24 = 13$,点$A_8$表示$13$,与原点距离$13$;
第9次移动:$13 - 27 = -14$,点$A_9$表示$-14$,与原点距离$14$;
第10次移动:$-14 + 30 = 16$,点$A_{10}$表示$16$,与原点距离$16$;
第11次移动:$16 - 33 = -17$,点$A_{11}$表示$-17$,与原点距离$17$;
第12次移动:$-17 + 36 = 19$,点$A_{12}$表示$19$,与原点距离$19$;
第13次移动:$19 - 39 = -20$,点$A_{13}$表示$-20$,与原点距离$20$。
$n$的最小值是$13$。
B
第1次移动:$1 - 3 = -2$,点$A_1$表示$-2$,与原点距离$2$;
第2次移动:$-2 + 6 = 4$,点$A_2$表示$4$,与原点距离$4$;
第3次移动:$4 - 9 = -5$,点$A_3$表示$-5$,与原点距离$5$;
第4次移动:$-5 + 12 = 7$,点$A_4$表示$7$,与原点距离$7$;
第5次移动:$7 - 15 = -8$,点$A_5$表示$-8$,与原点距离$8$;
第6次移动:$-8 + 18 = 10$,点$A_6$表示$10$,与原点距离$10$;
第7次移动:$10 - 21 = -11$,点$A_7$表示$-11$,与原点距离$11$;
第8次移动:$-11 + 24 = 13$,点$A_8$表示$13$,与原点距离$13$;
第9次移动:$13 - 27 = -14$,点$A_9$表示$-14$,与原点距离$14$;
第10次移动:$-14 + 30 = 16$,点$A_{10}$表示$16$,与原点距离$16$;
第11次移动:$16 - 33 = -17$,点$A_{11}$表示$-17$,与原点距离$17$;
第12次移动:$-17 + 36 = 19$,点$A_{12}$表示$19$,与原点距离$19$;
第13次移动:$19 - 39 = -20$,点$A_{13}$表示$-20$,与原点距离$20$。
$n$的最小值是$13$。
B
10. 有理数$5.6149$精确到百分位的近似数为
5.61
.答案:5.61
11. 据生物学统计,一个健康的成年女子体内的血量一般不低于 4000 毫升,每毫升血液中红细胞的数量约有$4.19× 10^{6}$个,因此,一个健康的成年女子体内的红细胞数量一般不低于
$1.676×10^{10}$
个(用科学记数法表示).答案:$1.676×10^{10}$
解析:
$4000×4.19×10^{6}=4×10^{3}×4.19×10^{6}=16.76×10^{9}=1.676×10^{10}$
12. 已知$a与b$互为倒数,$m与n$互为相反数,$x$的绝对值等于 1,那么$2025(m+n)-2025|x|+2026ab$的值为
1
.答案:1
解析:
因为$a$与$b$互为倒数,所以$ab = 1$;
因为$m$与$n$互为相反数,所以$m + n=0$;
因为$x$的绝对值等于$1$,所以$|x| = 1$。
则$2025(m + n)-2025|x| + 2026ab$
$=2025×0-2025×1 + 2026×1$
$=0-2025 + 2026$
$=1$
1
因为$m$与$n$互为相反数,所以$m + n=0$;
因为$x$的绝对值等于$1$,所以$|x| = 1$。
则$2025(m + n)-2025|x| + 2026ab$
$=2025×0-2025×1 + 2026×1$
$=0-2025 + 2026$
$=1$
1