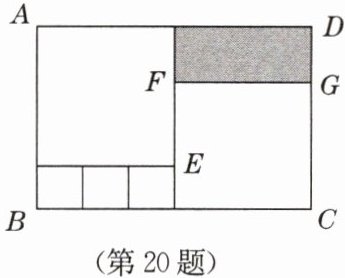
20. (6 分)如图,用三种大小不同的 5 个正方形和一个长方形(阴影部分)拼成长方形$ABCD$,其中$EF = 7\space cm$,最小的正方形的边长为$x\space cm$.
(1)$FG = $
(2)求长方形$ABCD$的周长(用含$x$的整式表示),当$x = 9$时,求其值.
(1)$FG = $
(7+x)
$cm$,$DG = $(3x-7)
$cm$(用含$x$的整式分别表示);(2)求长方形$ABCD$的周长(用含$x$的整式表示),当$x = 9$时,求其值.

(2)长方形的宽AB为:x+3x=4x(cm),长BC为:3x+x+7=(4x+7)(cm),则长方形ABCD的周长为:[4x+(4x+7)]×2=(16x+14)(cm). 当x=9时,16x+14=16×9+14=158(cm).
答案:(1)(7+x),(3x-7);(2)长方形的宽AB为:x+3x=4x(cm),长BC为:3x+x+7=(4x+7)(cm),则长方形ABCD的周长为:[4x+(4x+7)]×2=(16x+14)(cm). 当x=9时,16x+14=16×9+14=158(cm).
解析:
(1)$7 + x$,$3x - 7$;
(2)长方形的宽$AB$为:$x + 3x = 4x\ cm$,长$BC$为:$3x + x + 7 = (4x + 7)\ cm$,则长方形$ABCD$的周长为:$[4x + (4x + 7)] × 2 = (16x + 14)\ cm$。当$x = 9$时,$16x + 14 = 16 × 9 + 14 = 158\ cm$。
(2)长方形的宽$AB$为:$x + 3x = 4x\ cm$,长$BC$为:$3x + x + 7 = (4x + 7)\ cm$,则长方形$ABCD$的周长为:$[4x + (4x + 7)] × 2 = (16x + 14)\ cm$。当$x = 9$时,$16x + 14 = 16 × 9 + 14 = 158\ cm$。
21. (9 分)已知:$A = -x - 2y - 1$,$B = \frac{1}{2}x + y + 1$.
(1)求$A + 3B$;
(2)当$x + 2y = 6$时,求$A + 3B$的值;
(3)若$A + mB的值与y$的取值无关,求$m$的值.
(1)求$A + 3B$;
(2)当$x + 2y = 6$时,求$A + 3B$的值;
(3)若$A + mB的值与y$的取值无关,求$m$的值.
答案:(1)$\frac{1}{2}x+y+2$;(2)5;(3)m的值为2.
解析:
(1) $ A + 3B = (-x - 2y - 1) + 3\left(\frac{1}{2}x + y + 1\right) $
$ = -x - 2y - 1 + \frac{3}{2}x + 3y + 3 $
$ = \left(-x + \frac{3}{2}x\right) + (-2y + 3y) + (-1 + 3) $
$ = \frac{1}{2}x + y + 2 $
(2) 由
(1)知 $ A + 3B = \frac{1}{2}x + y + 2 $,因为 $ x + 2y = 6 $,所以 $ \frac{1}{2}(x + 2y) = 3 $,即 $ \frac{1}{2}x + y = 3 $,则 $ A + 3B = 3 + 2 = 5 $
(3) $ A + mB = (-x - 2y - 1) + m\left(\frac{1}{2}x + y + 1\right) $
$ = -x - 2y - 1 + \frac{m}{2}x + my + m $
$ = \left(-1 + \frac{m}{2}\right)x + (-2 + m)y + (-1 + m) $
因为 $ A + mB $ 的值与 $ y $ 的取值无关,所以 $ -2 + m = 0 $,解得 $ m = 2 $
22. (9 分)小敏和小华对一些四位数$\overline{abcd}$($a$,$b$,$c$,$d$均为不超过 9 的正整数)进行了观察、猜想,请你帮助他们一起完成探究.
(1)这个四位数可用含$a$,$b$,$c$,$d$的代数式表示为
(2)小敏尝试将一些四位数倒排后,再与原数相加,发现和都为 11 的倍数.
例如:$1234 + 4321 = 5555 = 505×11$,$4258 + 8524 = 12782 = 1162×11$.
你认为上述结论对于一般的$(\overline{abcd} + \overline{dcba})$也成立吗?请说明理由.
(3)小华猜想:若一个整数的奇位数字之和与偶位数字之和的差能被 11 整除,则这个数能被 11 整除.
例如:判断 491678 能不能被 11 整除.
奇位数字的和$8 + 6 + 9 = 23$,偶位数字的和$7 + 1 + 4 = 12$,$23 - 12 = 11$,因此,491678 能被 11 整除.这种方法叫奇偶位差法.
请你帮小华证明猜想:对于一个四位数$\overline{abcd}$($a$,$b$,$c$,$d$均为不超过 9 的正整数),若满足$(b + d) - (a + c) = 11$,则该四位数$\overline{abcd}$能被 11 整除.
(1)这个四位数可用含$a$,$b$,$c$,$d$的代数式表示为
1000a+100b+10c+d
.(2)小敏尝试将一些四位数倒排后,再与原数相加,发现和都为 11 的倍数.
例如:$1234 + 4321 = 5555 = 505×11$,$4258 + 8524 = 12782 = 1162×11$.
你认为上述结论对于一般的$(\overline{abcd} + \overline{dcba})$也成立吗?请说明理由.
能被11整除,理由如下:设四位数为$\overline{abcd}=1000a+100b+10c+d$,
∴$\overline{dcba}=1000d+100c+10b+a$,
∴$\overline{abcd}+\overline{dcba}=(1000a+100b+10c+d)+(1000d+100c+10b+a)=1001a+110b+110c+1001d=11×(91a+10b+10c+91d)$,
∴它们的和能被11整除.
∴$\overline{dcba}=1000d+100c+10b+a$,
∴$\overline{abcd}+\overline{dcba}=(1000a+100b+10c+d)+(1000d+100c+10b+a)=1001a+110b+110c+1001d=11×(91a+10b+10c+91d)$,
∴它们的和能被11整除.
(3)小华猜想:若一个整数的奇位数字之和与偶位数字之和的差能被 11 整除,则这个数能被 11 整除.
例如:判断 491678 能不能被 11 整除.
奇位数字的和$8 + 6 + 9 = 23$,偶位数字的和$7 + 1 + 4 = 12$,$23 - 12 = 11$,因此,491678 能被 11 整除.这种方法叫奇偶位差法.
请你帮小华证明猜想:对于一个四位数$\overline{abcd}$($a$,$b$,$c$,$d$均为不超过 9 的正整数),若满足$(b + d) - (a + c) = 11$,则该四位数$\overline{abcd}$能被 11 整除.
能被11整除,理由如下:$\overline{abcd}=1000a+100b+10c+d=a·(1001-1)+b·(99+1)+c·(11-1)+d=11×(91a+9b+c)+[(b+d)-(a+c)]$,
∵(b+d)-(a+c)=11=11×1,
∴$\overline{abcd}=11×(91a+9b+c)+11×1=11×(91a+9b+c+1)$,
∴四位数$\overline{abcd}$能被11整除.
∵(b+d)-(a+c)=11=11×1,
∴$\overline{abcd}=11×(91a+9b+c)+11×1=11×(91a+9b+c+1)$,
∴四位数$\overline{abcd}$能被11整除.
答案:(1)1000a+100b+10c+d;(2)能被11整除,理由如下:设四位数为$\overline{abcd}=1000a+100b+10c+d$,
∴$\overline{dcba}=1000d+100c+10b+a$,
∴$\overline{abcd}+\overline{dcba}=(1000a+100b+10c+d)+(1000d+100c+10b+a)=1001a+110b+110c+1001d=11×(91a+10b+10c+91d)$,
∴它们的和能被11整除.(3)能被11整除,理由如下:$\overline{abcd}=1000a+100b+10c+d=a·(1001-1)+b·(99+1)+c·(11-1)+d=11×(91a+9b+c)+[(b+d)-(a+c)]$,
∵(b+d)-(a+c)=11=11×1,
∴$\overline{abcd}=11×(91a+9b+c)+11×1=11×(91a+9b+c+1)$,
∴四位数$\overline{abcd}$能被11整除.
∴$\overline{dcba}=1000d+100c+10b+a$,
∴$\overline{abcd}+\overline{dcba}=(1000a+100b+10c+d)+(1000d+100c+10b+a)=1001a+110b+110c+1001d=11×(91a+10b+10c+91d)$,
∴它们的和能被11整除.(3)能被11整除,理由如下:$\overline{abcd}=1000a+100b+10c+d=a·(1001-1)+b·(99+1)+c·(11-1)+d=11×(91a+9b+c)+[(b+d)-(a+c)]$,
∵(b+d)-(a+c)=11=11×1,
∴$\overline{abcd}=11×(91a+9b+c)+11×1=11×(91a+9b+c+1)$,
∴四位数$\overline{abcd}$能被11整除.