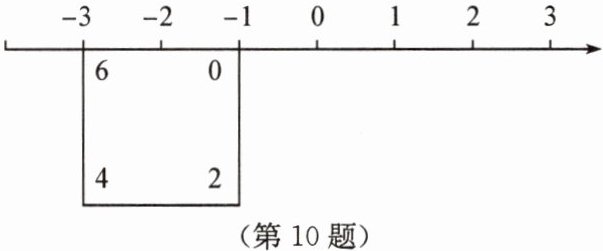
10. 如图,正方形的周长为8个单位长度.在该正方形的4个顶点处分别标上0,2,4,6,先让正方形上表示数字6的点与数轴上表示-3的点重合,再将数轴按顺时针方向环绕在该正方形上,则与数轴上表示2025的点重合的正方形上的点表示的数字为(
A.0
B.2
C.4
D.6
B
)
A.0
B.2
C.4
D.6
答案:B
解析:
正方形周长为8,边长为2,数字0,2,4,6按顺时针排列。6与-3重合,数轴顺时针环绕,周期为8。
2025 - (-3) = 2028,2028 ÷ 8 = 253……4,余数为4。
从6开始顺时针数4个单位:6→0→2→4→6,第4个为2。
B
2025 - (-3) = 2028,2028 ÷ 8 = 253……4,余数为4。
从6开始顺时针数4个单位:6→0→2→4→6,第4个为2。
B
11. 若x,y互为倒数,则$(-xy)^{2026}=$
1
.答案:1
解析:
因为$x$,$y$互为倒数,所以$xy = 1$。
则$(-xy)^{2026}=(-1)^{2026}=1$。
1
则$(-xy)^{2026}=(-1)^{2026}=1$。
1
12. 某日北京市的最低气温为-3℃,武汉市的最低气温为5℃,这一天北京市的最低气温比武汉市的最低气温低
8
℃.答案:8
解析:
5 - (-3) = 8
13. 在-0.4217中用数字3替换其中的一个非零数字,使所得的数最小,则被替换的数字是
2
.答案:2
解析:
将-0.4217中的非零数字4、2、1、7分别替换为3,得到:
-0.3217,-0.4317,-0.4237,-0.4213。
比较大小:-0.4317 < -0.4237 < -0.4213 < -0.3217。
最小的数是-0.4317,被替换的数字是2。
2
-0.3217,-0.4317,-0.4237,-0.4213。
比较大小:-0.4317 < -0.4237 < -0.4213 < -0.3217。
最小的数是-0.4317,被替换的数字是2。
2
14. 写出系数是-2,且只含有字母a,b的所有3次单项式:
$-2a^{2}b$,$-2ab^{2}$
.答案:$-2a^{2}b$,$-2ab^{2}$
15. 已知a+b= 8,则代数式1-2a-2b的值为
-15
.答案:$-15$
解析:
$1 - 2a - 2b = 1 - 2(a + b)$,
因为$a + b = 8$,
所以原式$= 1 - 2×8 = 1 - 16 = -15$。
$-15$
因为$a + b = 8$,
所以原式$= 1 - 2×8 = 1 - 16 = -15$。
$-15$
16. 数学课上老师讲了合并同类项,小玉回到家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现了一道题目:$(2a^2+3ab-b^2)-(-3a^2+ab+5b^2)= 5a^2$

+2ab
-6b^2,其中的一项被墨水弄脏了,则被墨水弄脏的一项是______.
答案:$+2ab$
解析:
$(2a^2 + 3ab - b^2) - (-3a^2 + ab + 5b^2)$
$=2a^2 + 3ab - b^2 + 3a^2 - ab - 5b^2$
$=(2a^2 + 3a^2) + (3ab - ab) + (-b^2 - 5b^2)$
$=5a^2 + 2ab - 6b^2$
$+2ab$
$=2a^2 + 3ab - b^2 + 3a^2 - ab - 5b^2$
$=(2a^2 + 3a^2) + (3ab - ab) + (-b^2 - 5b^2)$
$=5a^2 + 2ab - 6b^2$
$+2ab$
17. 当k=
-1
时,多项式$x^2-(k-1)xy-3y^2-2xy-5$中不含xy项.答案:$-1$
解析:
多项式$x^2-(k-1)xy-3y^2-2xy-5$合并同类项,得:
$x^2+[-(k-1)-2]xy-3y^2-5$
$=x^2+(-k+1-2)xy-3y^2-5$
$=x^2+(-k-1)xy-3y^2-5$
因为多项式不含$xy$项,所以$-k - 1 = 0$,解得$k=-1$。
$-1$
$x^2+[-(k-1)-2]xy-3y^2-5$
$=x^2+(-k+1-2)xy-3y^2-5$
$=x^2+(-k-1)xy-3y^2-5$
因为多项式不含$xy$项,所以$-k - 1 = 0$,解得$k=-1$。
$-1$
18. 数轴上在原点左边且距离原点2个单位长度的点所表示的数是
$-2$
.答案:$-2$
19. 已知$|x|= 7$,$|y|= 9$,且$|x-y|= y-x$,则$y^2+2x= $
95或67
.答案:95或67
解析:
因为$|x| = 7$,所以$x = \pm 7$;因为$|y| = 9$,所以$y = \pm 9$。
又因为$|x - y| = y - x$,所以$y - x \geq 0$,即$y \geq x$。
当$y = 9$时:
若$x = 7$,满足$9 \geq 7$,此时$y^2 + 2x = 9^2 + 2×7 = 81 + 14 = 95$;
若$x = -7$,满足$9 \geq -7$,此时$y^2 + 2x = 9^2 + 2×(-7) = 81 - 14 = 67$。
当$y = -9$时,无论$x = 7$还是$x = -7$,都有$-9 < 7$且$-9 < -7$,不满足$y \geq x$,故舍去。
综上,$y^2 + 2x = 95$或$67$。
95或67
又因为$|x - y| = y - x$,所以$y - x \geq 0$,即$y \geq x$。
当$y = 9$时:
若$x = 7$,满足$9 \geq 7$,此时$y^2 + 2x = 9^2 + 2×7 = 81 + 14 = 95$;
若$x = -7$,满足$9 \geq -7$,此时$y^2 + 2x = 9^2 + 2×(-7) = 81 - 14 = 67$。
当$y = -9$时,无论$x = 7$还是$x = -7$,都有$-9 < 7$且$-9 < -7$,不满足$y \geq x$,故舍去。
综上,$y^2 + 2x = 95$或$67$。
95或67
20. 按如图所示的程序计算,若开始输入的x的值为30,第1次得到的结果为15,第2次得到的结果为24……第2025次得到的结果为

12
.
答案:12
解析:
第1次:30为偶数,结果为$\frac{1}{2}×30 = 15$
第2次:15为奇数,结果为$15 + 9 = 24$
第3次:24为偶数,结果为$\frac{1}{2}×24 = 12$
第4次:12为偶数,结果为$\frac{1}{2}×12 = 6$
第5次:6为偶数,结果为$\frac{1}{2}×6 = 3$
第6次:3为奇数,结果为$3 + 9 = 12$
第7次:12为偶数,结果为$\frac{1}{2}×12 = 6$
第8次:6为偶数,结果为$\frac{1}{2}×6 = 3$
第9次:3为奇数,结果为$3 + 9 = 12$
……
从第3次开始,结果以12,6,3循环,周期为3
$(2025 - 2)÷3 = 2023÷3 = 674\cdots\cdots1$,余数为1
第2025次得到的结果为12
第2次:15为奇数,结果为$15 + 9 = 24$
第3次:24为偶数,结果为$\frac{1}{2}×24 = 12$
第4次:12为偶数,结果为$\frac{1}{2}×12 = 6$
第5次:6为偶数,结果为$\frac{1}{2}×6 = 3$
第6次:3为奇数,结果为$3 + 9 = 12$
第7次:12为偶数,结果为$\frac{1}{2}×12 = 6$
第8次:6为偶数,结果为$\frac{1}{2}×6 = 3$
第9次:3为奇数,结果为$3 + 9 = 12$
……
从第3次开始,结果以12,6,3循环,周期为3
$(2025 - 2)÷3 = 2023÷3 = 674\cdots\cdots1$,余数为1
第2025次得到的结果为12
21. (12分)计算:
(1)$(-3)^3÷2\frac{1}{4}+4-2^2×(-\frac{1}{3})$;
(2)$(\frac{1}{8}+1\frac{1}{3}-2.75)×(-24)+(-1)^{2026}$;
(3)$3(m-2n)-2(-2n+3m)$;
(4)$-5(a^2b-2ab^2)+3(3b^2a-2ba^2)$.
(1)$(-3)^3÷2\frac{1}{4}+4-2^2×(-\frac{1}{3})$;
(2)$(\frac{1}{8}+1\frac{1}{3}-2.75)×(-24)+(-1)^{2026}$;
(3)$3(m-2n)-2(-2n+3m)$;
(4)$-5(a^2b-2ab^2)+3(3b^2a-2ba^2)$.
答案:(1)$-6\frac{2}{3}$;(2)32;(3)$-3m-2n$;(4)$-11a^{2}b+19ab^{2}$
解析:
(1) $(-3)^3÷2\frac{1}{4}+4-2^2×(-\frac{1}{3})$
$=-27÷\frac{9}{4}+4-4×(-\frac{1}{3})$
$=-27×\frac{4}{9}+4+\frac{4}{3}$
$=-12+4+\frac{4}{3}$
$=-8+\frac{4}{3}$
$=-\frac{24}{3}+\frac{4}{3}$
$=-\frac{20}{3}=-6\frac{2}{3}$
(2) $(\frac{1}{8}+1\frac{1}{3}-2.75)×(-24)+(-1)^{2026}$
$=(\frac{1}{8}+\frac{4}{3}-\frac{11}{4})×(-24)+1$
$=\frac{1}{8}×(-24)+\frac{4}{3}×(-24)-\frac{11}{4}×(-24)+1$
$=-3-32+66+1$
$=(-3-32)+(66+1)$
$=-35+67=32$
(3) $3(m-2n)-2(-2n+3m)$
$=3m-6n+4n-6m$
$=(3m-6m)+(-6n+4n)$
$=-3m-2n$
(4) $-5(a^2b-2ab^2)+3(3b^2a-2ba^2)$
$=-5a^2b+10ab^2+9ab^2-6a^2b$
$=(-5a^2b-6a^2b)+(10ab^2+9ab^2)$
$=-11a^2b+19ab^2$