5. 小明学习了“等式的性质”后对小亮说:“我发现$4可以等于3$,你看这里有一个方程$4x - 2 = 3x - 2$,等式的两边都加上$2$,得$4x = 3x$,然后等式的两边都除以$x$,得$4 = 3$.”
(1)小明的说法对吗?为什么?
(2)你能求出方程$4x - 2 = 3x - 2$的解吗?
(1)小明的说法对吗?为什么?
(2)你能求出方程$4x - 2 = 3x - 2$的解吗?
答案:(1)不对.因为等式4x=3x中x的值为0,等式的两边不能同时除以0. (2)方程两边都加上2,得4x=3x,然后两边都减去3x,得x=0.
问题 已知$9m - 3n - 2025 = 0$,试求出$3m - n$的值.
名师指导
先利用等式的性质1,在等式两边同时加上$2025$,再利用等式的性质2,在等式两边同时除以$3$,即可求出$3m - n$的值.
解题示范(学生在教师指导下,独立完成)
解:
]
名师指导
先利用等式的性质1,在等式两边同时加上$2025$,再利用等式的性质2,在等式两边同时除以$3$,即可求出$3m - n$的值.
解题示范(学生在教师指导下,独立完成)
解:
]
答案:解:
由 $9m - 3n - 2025 = 0$,
根据等式的性质1,等式两边同时加上$2025$,得:
$9m - 3n = 2025$,
再根据等式的性质2,等式两边同时除以$3$,得:
$\frac{9m - 3n}{3} = \frac{2025}{3}$,
即:
$3m - n = 675$。
由 $9m - 3n - 2025 = 0$,
根据等式的性质1,等式两边同时加上$2025$,得:
$9m - 3n = 2025$,
再根据等式的性质2,等式两边同时除以$3$,得:
$\frac{9m - 3n}{3} = \frac{2025}{3}$,
即:
$3m - n = 675$。
1. 方程$1 - 3x = 0$的解是(
A.$x = -\frac{1}{3}$
B.$x= \frac{1}{3}$
C.$x = -3$
D.$x = 3$
B
)A.$x = -\frac{1}{3}$
B.$x= \frac{1}{3}$
C.$x = -3$
D.$x = 3$
答案:B.
解析:
解:$1 - 3x = 0$
$-3x = -1$
$x = \frac{1}{3}$
B.
$-3x = -1$
$x = \frac{1}{3}$
B.
2. 在中央电视台“开心辞典”节目中,某期的一道题目是:如图,两个天平都平衡,则1个苹果的重量是1个香蕉重量的(
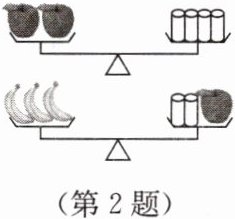
A.$\frac{2}{3}$倍
B.$\frac{4}{3}$倍
C.$\frac{3}{2}$倍
D.$2$倍
]
C
)
A.$\frac{2}{3}$倍
B.$\frac{4}{3}$倍
C.$\frac{3}{2}$倍
D.$2$倍
]
答案:C.
解析:
设1个苹果的重量为$x$,1个香蕉的重量为$y$,1个砝码的重量为$z$。
由第一个天平:$2x = 4z$,得$x = 2z$。
由第二个天平:$3y = 2z + x$,将$x = 2z$代入,得$3y = 2z + 2z = 4z$,即$y=\frac{4}{3}z$。
则$\frac{x}{y}=\frac{2z}{\frac{4}{3}z}=\frac{3}{2}$。
C.
由第一个天平:$2x = 4z$,得$x = 2z$。
由第二个天平:$3y = 2z + x$,将$x = 2z$代入,得$3y = 2z + 2z = 4z$,即$y=\frac{4}{3}z$。
则$\frac{x}{y}=\frac{2z}{\frac{4}{3}z}=\frac{3}{2}$。
C.
3. 已知等式$3a = 2b + 5$,则下列等式中不成立的是(
A.$3a - 5 = 2b$
B.$3a + 1 = 2b + 6$
C.$3ac = 2bc + 5$
D.$a= \frac{2}{3}b+\frac{5}{3}$
C
)A.$3a - 5 = 2b$
B.$3a + 1 = 2b + 6$
C.$3ac = 2bc + 5$
D.$a= \frac{2}{3}b+\frac{5}{3}$
答案:C.
解析:
A. 由$3a = 2b + 5$,等式两边同时减5,得$3a - 5 = 2b$,成立;
B. 由$3a = 2b + 5$,等式两边同时加1,得$3a + 1 = 2b + 6$,成立;
C. 由$3a = 2b + 5$,等式两边同时乘$c$,得$3ac = 2bc + 5c$,原选项$3ac = 2bc + 5$不成立;
D. 由$3a = 2b + 5$,等式两边同时除以3,得$a = \frac{2}{3}b + \frac{5}{3}$,成立。
C
B. 由$3a = 2b + 5$,等式两边同时加1,得$3a + 1 = 2b + 6$,成立;
C. 由$3a = 2b + 5$,等式两边同时乘$c$,得$3ac = 2bc + 5c$,原选项$3ac = 2bc + 5$不成立;
D. 由$3a = 2b + 5$,等式两边同时除以3,得$a = \frac{2}{3}b + \frac{5}{3}$,成立。
C
4. 某城市平均每天产生生活垃圾$700t$,由甲、乙两个垃圾处理厂处理.已知甲厂每小时可处理垃圾$55t$,乙厂每小时可处理垃圾$45t$.甲、乙两厂同时处理该城市的生活垃圾,每天需多长时间才能处理完?
答案:7 h.
解析:
设每天需$x$小时才能处理完。
甲厂每小时处理$55t$,$x$小时处理$55x t$;乙厂每小时处理$45t$,$x$小时处理$45x t$。
根据题意,可列方程:$55x + 45x = 700$
合并同类项得:$100x = 700$
解得:$x = 7$
7 h.
甲厂每小时处理$55t$,$x$小时处理$55x t$;乙厂每小时处理$45t$,$x$小时处理$45x t$。
根据题意,可列方程:$55x + 45x = 700$
合并同类项得:$100x = 700$
解得:$x = 7$
7 h.