3. 某城市平均每天产生垃圾 700 吨,由甲、乙两个垃圾处理厂处理. 已知甲厂每小时可处理垃圾 55 吨,每吨需费用 10 元;乙厂每小时可处理垃圾 45 吨,每吨需费用 11 元.
(1)甲、乙两厂同时处理该城市的垃圾,每天需多少时间完成?
(2)如果该城市每天用于处理垃圾的费用为 7 300 元,那么甲厂每天处理垃圾多少吨?
(1)甲、乙两厂同时处理该城市的垃圾,每天需多少时间完成?
(2)如果该城市每天用于处理垃圾的费用为 7 300 元,那么甲厂每天处理垃圾多少吨?
答案:(1)甲、乙两厂同时处理该城市的垃圾,每天需7小时完成;(2)甲厂每天处理垃圾400吨
解析:
(1)设每天需$x$小时完成,根据题意得:$(55 + 45)x=700$,解得$x = 7$,答:每天需7小时完成;
(2)设甲厂每天处理垃圾$y$吨,根据题意得:$10y+11(700 - y)=7300$,解得$y = 400$,答:甲厂每天处理垃圾400吨。
(2)设甲厂每天处理垃圾$y$吨,根据题意得:$10y+11(700 - y)=7300$,解得$y = 400$,答:甲厂每天处理垃圾400吨。
4. 某地为了打造风光带,将一段长为 360 m 的河道整治任务交由甲、乙两个工程队先后接力完成,共用时 20 天. 已知甲工程队每天整治 24 m,乙工程队每天整治 16 m. 求甲、乙两个工程队分别整治了多长的河道.
答案:解:设甲队整治了x天,则乙队整治了(20-x)天. 由题意,得24x+16(20-x)=360,解得x=5,
∴ 乙队整治了20-5=15(天),
∴ 甲队整治的河道长为24×5=120(m),乙队整治的河道长为16×15=240(m). 答:甲、乙两个工程队分别整治了120 m,240 m.
∴ 乙队整治了20-5=15(天),
∴ 甲队整治的河道长为24×5=120(m),乙队整治的河道长为16×15=240(m). 答:甲、乙两个工程队分别整治了120 m,240 m.
“幸福是奋斗出来的”,在数轴上,若点 $ C $ 到点 $ A $ 的距离刚好是 3,则点 $ C $ 叫作点 $ A $ 的“幸福点”,若点 $ C $ 到点 $ A $,$ B $ 的距离之和为 6,则点 $ C $ 叫作 $ A $,$ B $ 的“幸福中心”.
(1)如图(1),点 $ A $ 表示的数为 $ -1 $,则点 $ A $ 的“幸福点”$ C $ 所表示的数应该是
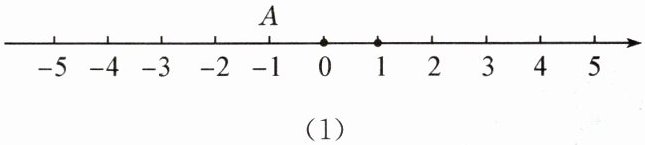
(2)如图(2),点 $ M $,$ N $ 为数轴上两点,点 $ M $ 所表示的数为 4,点 $ N $ 所表示的数为 $ -2 $,点 $ C $ 是点 $ M $,$ N $ 的“幸福中心”,则点 $ C $ 所表示的数可以是

(3)如图(3),$ A $,$ B $,$ P $ 为数轴上三点,点 $ A $ 所表示的数为 $ -1 $,点 $ B $ 所表示的数为 4,点 $ P $ 所表示的数为 8. 现有一只电子蚂蚁从点 $ P $ 出发,以 2 个单位/秒的速度向左运动,当经过多少秒时,电子蚂蚁是点 $ A $ 和 $ B $ 的“幸福中心”?
]

(1)如图(1),点 $ A $ 表示的数为 $ -1 $,则点 $ A $ 的“幸福点”$ C $ 所表示的数应该是
-4或2
;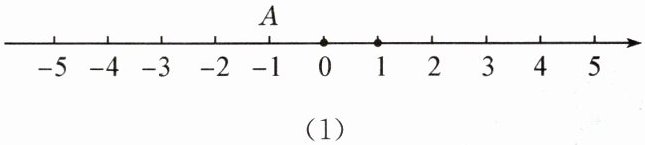
(2)如图(2),点 $ M $,$ N $ 为数轴上两点,点 $ M $ 所表示的数为 4,点 $ N $ 所表示的数为 $ -2 $,点 $ C $ 是点 $ M $,$ N $ 的“幸福中心”,则点 $ C $ 所表示的数可以是
0
(填一个即可);
(3)如图(3),$ A $,$ B $,$ P $ 为数轴上三点,点 $ A $ 所表示的数为 $ -1 $,点 $ B $ 所表示的数为 4,点 $ P $ 所表示的数为 8. 现有一只电子蚂蚁从点 $ P $ 出发,以 2 个单位/秒的速度向左运动,当经过多少秒时,电子蚂蚁是点 $ A $ 和 $ B $ 的“幸福中心”?
]

经过1.75 s或4.75 s时,电子蚂蚁是点A和B的“幸福中心”.
答案:解:(1)-4或2;(2)0(答案不唯一);(3)经过1.75 s或4.75 s时,电子蚂蚁是点A和B的“幸福中心”.
解析:
(1)-4或2;
(2)0(答案不唯一);
(3)设经过$ t $秒时,电子蚂蚁是点$ A $和$ B $的“幸福中心”,电子蚂蚁表示的数为$ 8 - 2t $。
当电子蚂蚁在点$ A $左侧时,$(-1)-(8 - 2t)+4-(8 - 2t)=6$,解得$ t = \frac{19}{4}=4.75$;
当电子蚂蚁在点$ B $右侧时,$(8 - 2t)-(-1)+(8 - 2t)-4=6$,解得$ t = \frac{7}{4}=1.75$;
当电子蚂蚁在$ A $、$ B $之间时,$4 - (-1)=5\neq6$,无解。
综上,$ t = 1.75 $或$ t = 4.75 $。
(2)0(答案不唯一);
(3)设经过$ t $秒时,电子蚂蚁是点$ A $和$ B $的“幸福中心”,电子蚂蚁表示的数为$ 8 - 2t $。
当电子蚂蚁在点$ A $左侧时,$(-1)-(8 - 2t)+4-(8 - 2t)=6$,解得$ t = \frac{19}{4}=4.75$;
当电子蚂蚁在点$ B $右侧时,$(8 - 2t)-(-1)+(8 - 2t)-4=6$,解得$ t = \frac{7}{4}=1.75$;
当电子蚂蚁在$ A $、$ B $之间时,$4 - (-1)=5\neq6$,无解。
综上,$ t = 1.75 $或$ t = 4.75 $。