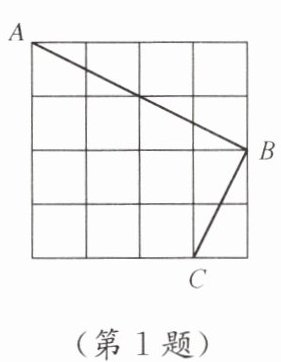
1. 如图是由边长为 1 m 的正方形地砖铺设的地面.一只蚂蚁沿图中“A→B→C”的线路爬行,则蚂蚁沿该线路从点 A 爬行到点 C 的路程为
$5+\sqrt{5}$
m.(结果保留根号)
答案:$5+\sqrt{5}$。
解析:
由图可知,A、B、C均在边长为1m的正方形地砖的顶点上。
从A到B的水平距离为3个正方形边长,垂直距离为4个正方形边长,
即$AB=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$(m)。
从B到C的水平距离为2个正方形边长,垂直距离为1个正方形边长,
即$BC=\sqrt{2^2+1^2}=\sqrt{4+1}=\sqrt{5}$(m)。
因此,从A到C的总路程为$AB+BC=5+\sqrt{5}$(m)。
从A到B的水平距离为3个正方形边长,垂直距离为4个正方形边长,
即$AB=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$(m)。
从B到C的水平距离为2个正方形边长,垂直距离为1个正方形边长,
即$BC=\sqrt{2^2+1^2}=\sqrt{4+1}=\sqrt{5}$(m)。
因此,从A到C的总路程为$AB+BC=5+\sqrt{5}$(m)。
2. 如图,有一个绳索拉直的秋千,绳索 AB 的长度为 5 m,若将木板往水平方向向前推进 3 m(即 DE= 3 m),且绳索保持拉直的状态,则此时木板上升的高度为

1
m.
答案:1
解析:
设木板原位置为点B,推进后为点C,过点C作CE垂直地面于E,过点B作BD垂直地面于D,连接AC,AB。则AC=AB=5m,CD=DE=3m(此处修正:应为CE=3m,BD=CE=3m,设木板上升高度为h,即BC=h,AD=AB=5m,AE=AD-DE=5-h,在Rt△ACE中,AC²=AE²+CE²,即5²=(5-h)²+3²,25=25-10h+h²+9,h²-10h+9=0,(h-1)(h-9)=0,解得h=1或h=9(舍去),故h=1m。
3. 如图,△ABE,△BCF,△CDG,△DAH 是四个全等的直角三角形,其中,AE= 5,AB= 13,EG 的长为______

7√2
.
答案:7√2
解析:
∵△ABE是直角三角形,AE=5,AB=13,
∴由勾股定理得:BE=√(AB²-AE²)=√(13²-5²)=12。
∵四个直角三角形全等,∴每个直角三角形两直角边分别为5和12。
观察图形,四个直角三角形围成中间的四边形EFGH,其边长为两直角边之差:12-5=7,即四边形EFGH是边长为7的正方形。
∴EG是正方形EFGH的对角线,EG=7√2。
∴由勾股定理得:BE=√(AB²-AE²)=√(13²-5²)=12。
∵四个直角三角形全等,∴每个直角三角形两直角边分别为5和12。
观察图形,四个直角三角形围成中间的四边形EFGH,其边长为两直角边之差:12-5=7,即四边形EFGH是边长为7的正方形。
∴EG是正方形EFGH的对角线,EG=7√2。
4. 某工厂的大门形状如图所示(大门上方为半圆),现有四辆装满货物的卡车,外形宽都是2.0 m,高分别为 2.8 m,3.1 m,3.4 m,3.7 m,则能通过该工厂大门的车辆数是(参考数据:√2≈1.41,√3≈1.73,√5≈2.24) (

A.1
B.2
C.3
D.4
B
)
A.1
B.2
C.3
D.4
答案:B
解析:
大门宽4.0m,上方半圆半径r=2.0m,下方矩形高1.6m。卡车宽2.0m,从中间通过时,卡车边缘距圆心水平距离d=(4.0-2.0)/2=1.0m。在半圆中,由勾股定理得半圆部分允许高度h=√(r²-d²)=√(2²-1²)=√3≈1.73m。总允许高度为1.6+1.73≈3.33m。卡车高2.8m、3.1m≤3.33m可通过,3.4m、3.7m>3.33m不可通过,能通过2辆。
5. 已知:如图,在四边形 ABCD 中,连接 AC,AB= 12,BC= 9,CD= 8,AD= 17,∠B= 90°.
求证:△ACD 是直角三角形.

求证:△ACD 是直角三角形.

答案:因为$\angle B=90^{\circ}$,所以在$Rt\triangle ABC$中,根据勾股定理$AC^{2}=AB^{2}+BC^{2}$。
已知$AB = 12$,$BC = 9$,则$AC^{2}=12^{2}+9^{2}=144 + 81=225$,所以$AC = 15$。
在$\triangle ACD$中,$AC = 15$,$CD = 8$,$AD = 17$。
计算$AC^{2}+CD^{2}=15^{2}+8^{2}=225 + 64 = 289$,而$AD^{2}=17^{2}=289$。
所以$AC^{2}+CD^{2}=AD^{2}$,根据勾股定理的逆定理,$\angle ACD = 90^{\circ}$,即$\triangle ACD$是直角三角形。
已知$AB = 12$,$BC = 9$,则$AC^{2}=12^{2}+9^{2}=144 + 81=225$,所以$AC = 15$。
在$\triangle ACD$中,$AC = 15$,$CD = 8$,$AD = 17$。
计算$AC^{2}+CD^{2}=15^{2}+8^{2}=225 + 64 = 289$,而$AD^{2}=17^{2}=289$。
所以$AC^{2}+CD^{2}=AD^{2}$,根据勾股定理的逆定理,$\angle ACD = 90^{\circ}$,即$\triangle ACD$是直角三角形。
6. 细心观察图形,认真分析各式,解答下列问题:
$OA_2^2= (√1)^2+1= 2,S_1= √1/2;OA_3^2= 1^2+(√2)^2= 3,S_2= √2/2;OA_4^2= 1^2+(√3)^2= 4,S_3= √3/2;…$
(1)请用含有 n(n 是正整数)的等式表示上述式子的规律$:OAₙ^2= $
(2)求$ OA_1₀$的长.
(3)若一个三角形的面积是√5,它是第几个三角形?
(4)求$ S_1^2+S_2^2+S_3^2+…+S_1₀^2$的值.
$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots +S_{10}^{2}=(\frac{\sqrt{1}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}+\cdots +(\frac{\sqrt{10}}{2})^{2}$
$=\frac{1}{4}(1 + 2+3+\cdots + 10)=\frac{1}{4}×\frac{10×(10 + 1)}{2}=\frac{55}{4}$
$OA_2^2= (√1)^2+1= 2,S_1= √1/2;OA_3^2= 1^2+(√2)^2= 3,S_2= √2/2;OA_4^2= 1^2+(√3)^2= 4,S_3= √3/2;…$
(1)请用含有 n(n 是正整数)的等式表示上述式子的规律$:OAₙ^2= $
n
,$Sₙ= $$\frac{\sqrt{n}}{2}$
.(2)求$ OA_1₀$的长.
因为$OA_{n}^{2}=n$,当$n = 10$时,$OA_{10}^{2}=10$,所以$OA_{10}=\sqrt{10}$
(3)若一个三角形的面积是√5,它是第几个三角形?
已知$S_{n}=\frac{\sqrt{n}}{2}$,若$S_{n}=\sqrt{5}$,则$\frac{\sqrt{n}}{2}=\sqrt{5}$,$\sqrt{n}=2\sqrt{5}=\sqrt{20}$,所以$n = 20$,即它是第$20$个三角形
(4)求$ S_1^2+S_2^2+S_3^2+…+S_1₀^2$的值.
$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots +S_{10}^{2}=(\frac{\sqrt{1}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}+\cdots +(\frac{\sqrt{10}}{2})^{2}$
$=\frac{1}{4}(1 + 2+3+\cdots + 10)=\frac{1}{4}×\frac{10×(10 + 1)}{2}=\frac{55}{4}$
答案:(1)
$OA_{n}^{2}=n$,$S_{n}=\frac{\sqrt{n}}{2}$
(2)
因为$OA_{n}^{2}=n$,当$n = 10$时,$OA_{10}^{2}=10$,所以$OA_{10}=\sqrt{10}$
(3)
已知$S_{n}=\frac{\sqrt{n}}{2}$,若$S_{n}=\sqrt{5}$,则$\frac{\sqrt{n}}{2}=\sqrt{5}$,$\sqrt{n}=2\sqrt{5}=\sqrt{20}$,所以$n = 20$,即它是第$20$个三角形
(4)
$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots +S_{10}^{2}=(\frac{\sqrt{1}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}+\cdots +(\frac{\sqrt{10}}{2})^{2}$
$=\frac{1}{4}(1 + 2+3+\cdots + 10)=\frac{1}{4}×\frac{10×(10 + 1)}{2}=\frac{55}{4}$
$OA_{n}^{2}=n$,$S_{n}=\frac{\sqrt{n}}{2}$
(2)
因为$OA_{n}^{2}=n$,当$n = 10$时,$OA_{10}^{2}=10$,所以$OA_{10}=\sqrt{10}$
(3)
已知$S_{n}=\frac{\sqrt{n}}{2}$,若$S_{n}=\sqrt{5}$,则$\frac{\sqrt{n}}{2}=\sqrt{5}$,$\sqrt{n}=2\sqrt{5}=\sqrt{20}$,所以$n = 20$,即它是第$20$个三角形
(4)
$S_{1}^{2}+S_{2}^{2}+S_{3}^{2}+\cdots +S_{10}^{2}=(\frac{\sqrt{1}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{3}}{2})^{2}+\cdots +(\frac{\sqrt{10}}{2})^{2}$
$=\frac{1}{4}(1 + 2+3+\cdots + 10)=\frac{1}{4}×\frac{10×(10 + 1)}{2}=\frac{55}{4}$
解析:
(1) $OA_n^2 = n$,$S_n = \frac{\sqrt{n}}{2}$
(2) 由
(1)知$OA_n^2 = n$,当$n = 10$时,$OA_{10}^2 = 10$,则$OA_{10} = \sqrt{10}$
(3) 由$S_n = \frac{\sqrt{n}}{2} = \sqrt{5}$,得$\sqrt{n} = 2\sqrt{5} = \sqrt{20}$,所以$n = 20$
(4) $S_1^2 + S_2^2 + \cdots + S_{10}^2 = \left(\frac{\sqrt{1}}{2}\right)^2 + \left(\frac{\sqrt{2}}{2}\right)^2 + \cdots + \left(\frac{\sqrt{10}}{2}\right)^2 = \frac{1 + 2 + \cdots + 10}{4} = \frac{55}{4}$