1. 如图①是我国古代著名的“赵爽弦图”的示意图,由四个全等的直角三角形围成.若 AC= 2,BC= 3,将四个直角三角形中边长为 3 的直角边分别向外延长一倍,得到如图②所示的“风车”,则这个“风车”的周长是

8√10
.
答案:8√10
解析:
由题意,每个直角三角形的两条直角边分别为AC=2,BC=3。将边长为3的直角边向外延长一倍,延长后长度为3×2=6。延长后形成的新直角三角形的两条直角边分别为2和6,其斜边长为√(2²+6²)=√40=2√10。“风车”由4个这样的斜边构成周长,故周长为4×2√10=8√10。
2. 在我国古代数学著作《九章算术》“勾股”章中有一题:“今有开门去阃(kǔn)一尺,不合二寸,问门广几何?”大意是说:如图,推开双门(AD 和 BC),门边缘 D,C 两点到门槛 AB 的距离为1 尺(1 尺= 10 寸),双门间的缝隙 CD 为 2 寸,那么门的宽度(两扇门的和)AB为

101
寸.
答案:101
解析:
设门的宽度为$AB = L$寸,过$D$、$C$作$AB$的垂线,垂足分别为$E$、$F$,则$DE = CF = 10$寸(1尺=10寸),$CD = 2$寸。由对称性知$AE = FB$,设$AE = FB = y$,则$EF = CD = 2$寸,故$AB = AE + EF + FB = 2y + 2$,即$y = \frac{L - 2}{2}$。
因$AD$、$BC$为门的宽度(每扇门宽$\frac{L}{2}$寸),在$Rt\triangle ADE$中,$AD^2 = AE^2 + DE^2$,即$(\frac{L}{2})^2 = y^2 + 10^2$。
代入$y = \frac{L - 2}{2}$,得$(\frac{L}{2})^2 = (\frac{L - 2}{2})^2 + 100$。
展开解得:$L^2 = (L - 2)^2 + 400$,$L^2 = L^2 - 4L + 4 + 400$,$4L = 404$,$L = 101$。
因$AD$、$BC$为门的宽度(每扇门宽$\frac{L}{2}$寸),在$Rt\triangle ADE$中,$AD^2 = AE^2 + DE^2$,即$(\frac{L}{2})^2 = y^2 + 10^2$。
代入$y = \frac{L - 2}{2}$,得$(\frac{L}{2})^2 = (\frac{L - 2}{2})^2 + 100$。
展开解得:$L^2 = (L - 2)^2 + 400$,$L^2 = L^2 - 4L + 4 + 400$,$4L = 404$,$L = 101$。
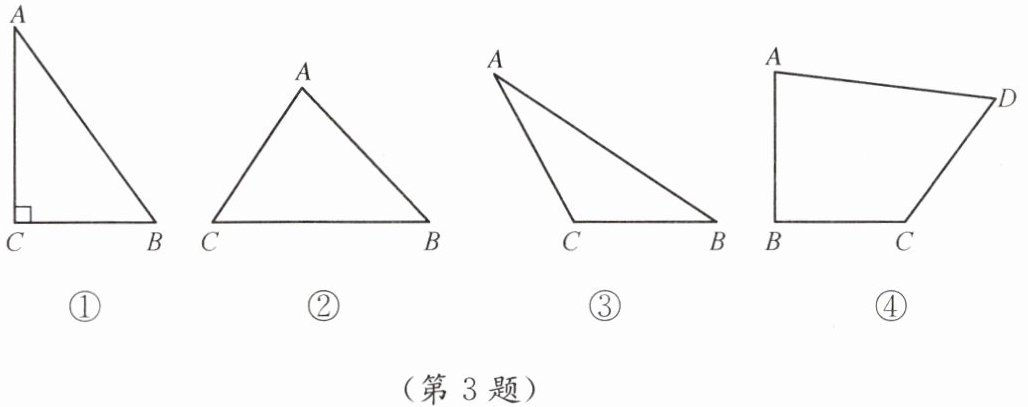
3. 在△ABC 中,AB= c,BC= a,AC= b.如图①,若∠C= 90°时,根据勾股定理有$ a^2+b^2= c^2.$
(1)如图②,当△ABC 为锐角三角形时,类比勾股定理,判断$ a^2+b^2$与$ c^2$的大小关系,并证明;
(2)如图③,当△ABC 为钝角三角形时,类比勾股定理,判断$ a^2+b^2$与$ c^2$的大小关系,并证明;
(3)如图④,一块四边形的试验田 ABCD,已知∠B= 90°,AB= 80 m,BC= 60 m,CD= 90 m,AD= 110 m,求这块试验田的面积.
(1)如图②,当△ABC 为锐角三角形时,类比勾股定理,判断$ a^2+b^2$与$ c^2$的大小关系,并证明;
(2)如图③,当△ABC 为钝角三角形时,类比勾股定理,判断$ a^2+b^2$与$ c^2$的大小关系,并证明;
(3)如图④,一块四边形的试验田 ABCD,已知∠B= 90°,AB= 80 m,BC= 60 m,CD= 90 m,AD= 110 m,求这块试验田的面积.

答案:(1) $a^2 + b^2 > c^2$。
证明:过点$A$作$AD \perp BC$于点$D$。
设$CD = x$,则$BD = a - x$。
在$Rt\triangle ADC$中,$AD^2 = b^2 - x^2$;在$Rt\triangle ADB$中,$AD^2 = c^2 - (a - x)^2$。
所以$b^2 - x^2 = c^2 - (a - x)^2$,展开得$b^2 - x^2 = c^2 - a^2 + 2ax - x^2$,移项可得$a^2 + b^2 - c^2 = 2ax$。
因为$a>0$,$x>0$,所以$2ax>0$,即$a^2 + b^2 - c^2>0$,所以$a^2 + b^2 > c^2$。
(2) $a^2 + b^2 < c^2$。
证明:过点$A$作$AD \perp BC$交$BC$的延长线于点$D$。
设$CD = x$,则$BD = a + x$。
在$Rt\triangle ADC$中,$AD^2 = b^2 - x^2$;在$Rt\triangle ADB$中,$AD^2 = c^2 - (a + x)^2$。
所以$b^2 - x^2 = c^2 - (a + x)^2$,展开得$b^2 - x^2 = c^2 - a^2 - 2ax - x^2$,移项可得$a^2 + b^2 - c^2 = -2ax$。
因为$a>0$,$x>0$,所以$-2ax<0$,即$a^2 + b^2 - c^2<0$,所以$a^2 + b^2 < c^2$。
(3) 连接$AC$。
在$Rt\triangle ABC$中,$AC^2 = AB^2 + BC^2 = 80^2 + 60^2 = 10000$,所以$AC = 100m$。
在$\triangle ACD$中,$AC^2 + CD^2 = 10000 + 8100 = 18100$,$AD^2 = 110^2 = 12100$,因为$18100>12100$,即$AC^2 + CD^2 > AD^2$。
又因为$AC^2+AD^2=10000 + 12100=22100$,$CD^2 = 8100$,$22100>8100$,即$AC^2+AD^2>CD^2$,且$AD^2 + CD^2 = 12100 + 8100 = 20200$,$AC^2 = 10000$,$20200>10000$,即$AD^2 + CD^2 > AC^2$,所以$\angle ACD$是钝角,根据(2)的结论$AC^2 + CD^2 < AD^2$时才是钝角三角形,这里我们用余弦定理判断$\angle ACD$余弦值$\cos\angle ACD=\frac{AC^{2}+CD^{2}-AD^{2}}{2\cdot AC\cdot CD}=\frac{10000 + 8100-12100}{2×100×90}=\frac{1}{3}>0$,$\angle ACD$是锐角,再判断$\angle CAD$,$\cos\angle CAD=\frac{AC^{2}+AD^{2}-CD^{2}}{2\cdot AC\cdot AD}=\frac{10000+12100 - 8100}{2×100×110}=\frac{7}{11}>0$,$\angle CAD$是锐角,$\angle ADC$余弦值$\cos\angle ADC=\frac{AD^{2}+CD^{2}-AC^{2}}{2\cdot AD\cdot CD}=\frac{12100 + 8100-10000}{2×110×90}=\frac{17}{33}>0$,$\angle ADC$是锐角,我们可通过$AC^{2}+CD^{2}=18100$,$AD^{2}=12100$,$AC^{2}+CD^{2}-AD^{2}=6000>0$,再用海伦公式判断不太方便,我们用面积法,先求$\triangle ACD$面积,根据$S_{\triangle ACD}=\sqrt{p(p - a)(p - b)(p - c)}$($p=\frac{AC + CD+AD}{2}=\frac{100 + 90+110}{2}=150$),$S_{\triangle ACD}=\sqrt{150(150 - 100)(150 - 90)(150 - 110)}=\sqrt{150×50×60×40}=\sqrt{18000000}=3000\sqrt{2}$,$S_{\triangle ABC}=\frac{1}{2}× AB× BC=\frac{1}{2}×80×60 = 2400$。
四边形$ABCD$面积$S = S_{\triangle ABC}+S_{\triangle ACD}=2400+3000\sqrt{2}= 3900 + 3000\sqrt{2}(m^2)$(这里也可通过勾股定理逆定理判断$\triangle ACD$形状,$AC = 100m$,$CD = 90m$,$AD = 110m$,$AC^{2}+CD^{2}=10000 + 8100=18100$,$AD^{2}=12100$,$AC^{2}+CD^{2}-AD^{2}=6000>0$,再用余弦定理求角判断形状后求面积,$\triangle ABC$面积$S_1=\frac{1}{2}×60×80 = 2400$,对于$\triangle ACD$,根据$S=\sqrt{s(s - a)(s - b)(s - c)}$($s=\frac{100 + 90+110}{2}=150$)得$S_2=\sqrt{150×(150 - 100)×(150 - 90)×(150 - 110)} = 3000\sqrt{2}$,总面积$S = 2400+3000\sqrt{2}$)。
综上,答案依次为:(1)$a^2 + b^2 > c^2$,证明见上述过程;(2)$a^2 + b^2 < c^2$,证明见上述过程;(3)$(3900 + 3000\sqrt{2})m^2$。
证明:过点$A$作$AD \perp BC$于点$D$。
设$CD = x$,则$BD = a - x$。
在$Rt\triangle ADC$中,$AD^2 = b^2 - x^2$;在$Rt\triangle ADB$中,$AD^2 = c^2 - (a - x)^2$。
所以$b^2 - x^2 = c^2 - (a - x)^2$,展开得$b^2 - x^2 = c^2 - a^2 + 2ax - x^2$,移项可得$a^2 + b^2 - c^2 = 2ax$。
因为$a>0$,$x>0$,所以$2ax>0$,即$a^2 + b^2 - c^2>0$,所以$a^2 + b^2 > c^2$。
(2) $a^2 + b^2 < c^2$。
证明:过点$A$作$AD \perp BC$交$BC$的延长线于点$D$。
设$CD = x$,则$BD = a + x$。
在$Rt\triangle ADC$中,$AD^2 = b^2 - x^2$;在$Rt\triangle ADB$中,$AD^2 = c^2 - (a + x)^2$。
所以$b^2 - x^2 = c^2 - (a + x)^2$,展开得$b^2 - x^2 = c^2 - a^2 - 2ax - x^2$,移项可得$a^2 + b^2 - c^2 = -2ax$。
因为$a>0$,$x>0$,所以$-2ax<0$,即$a^2 + b^2 - c^2<0$,所以$a^2 + b^2 < c^2$。
(3) 连接$AC$。
在$Rt\triangle ABC$中,$AC^2 = AB^2 + BC^2 = 80^2 + 60^2 = 10000$,所以$AC = 100m$。
在$\triangle ACD$中,$AC^2 + CD^2 = 10000 + 8100 = 18100$,$AD^2 = 110^2 = 12100$,因为$18100>12100$,即$AC^2 + CD^2 > AD^2$。
又因为$AC^2+AD^2=10000 + 12100=22100$,$CD^2 = 8100$,$22100>8100$,即$AC^2+AD^2>CD^2$,且$AD^2 + CD^2 = 12100 + 8100 = 20200$,$AC^2 = 10000$,$20200>10000$,即$AD^2 + CD^2 > AC^2$,所以$\angle ACD$是钝角,根据(2)的结论$AC^2 + CD^2 < AD^2$时才是钝角三角形,这里我们用余弦定理判断$\angle ACD$余弦值$\cos\angle ACD=\frac{AC^{2}+CD^{2}-AD^{2}}{2\cdot AC\cdot CD}=\frac{10000 + 8100-12100}{2×100×90}=\frac{1}{3}>0$,$\angle ACD$是锐角,再判断$\angle CAD$,$\cos\angle CAD=\frac{AC^{2}+AD^{2}-CD^{2}}{2\cdot AC\cdot AD}=\frac{10000+12100 - 8100}{2×100×110}=\frac{7}{11}>0$,$\angle CAD$是锐角,$\angle ADC$余弦值$\cos\angle ADC=\frac{AD^{2}+CD^{2}-AC^{2}}{2\cdot AD\cdot CD}=\frac{12100 + 8100-10000}{2×110×90}=\frac{17}{33}>0$,$\angle ADC$是锐角,我们可通过$AC^{2}+CD^{2}=18100$,$AD^{2}=12100$,$AC^{2}+CD^{2}-AD^{2}=6000>0$,再用海伦公式判断不太方便,我们用面积法,先求$\triangle ACD$面积,根据$S_{\triangle ACD}=\sqrt{p(p - a)(p - b)(p - c)}$($p=\frac{AC + CD+AD}{2}=\frac{100 + 90+110}{2}=150$),$S_{\triangle ACD}=\sqrt{150(150 - 100)(150 - 90)(150 - 110)}=\sqrt{150×50×60×40}=\sqrt{18000000}=3000\sqrt{2}$,$S_{\triangle ABC}=\frac{1}{2}× AB× BC=\frac{1}{2}×80×60 = 2400$。
四边形$ABCD$面积$S = S_{\triangle ABC}+S_{\triangle ACD}=2400+3000\sqrt{2}= 3900 + 3000\sqrt{2}(m^2)$(这里也可通过勾股定理逆定理判断$\triangle ACD$形状,$AC = 100m$,$CD = 90m$,$AD = 110m$,$AC^{2}+CD^{2}=10000 + 8100=18100$,$AD^{2}=12100$,$AC^{2}+CD^{2}-AD^{2}=6000>0$,再用余弦定理求角判断形状后求面积,$\triangle ABC$面积$S_1=\frac{1}{2}×60×80 = 2400$,对于$\triangle ACD$,根据$S=\sqrt{s(s - a)(s - b)(s - c)}$($s=\frac{100 + 90+110}{2}=150$)得$S_2=\sqrt{150×(150 - 100)×(150 - 90)×(150 - 110)} = 3000\sqrt{2}$,总面积$S = 2400+3000\sqrt{2}$)。
综上,答案依次为:(1)$a^2 + b^2 > c^2$,证明见上述过程;(2)$a^2 + b^2 < c^2$,证明见上述过程;(3)$(3900 + 3000\sqrt{2})m^2$。