活动一:试一试 做一做
1. 数形结合思想的运用.
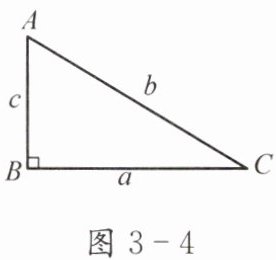
(1)如图 3-4,在△ABC 中,∠B= 90°,一直角边为 a,斜边为 b,则另一直角边 c 满足$c^{2}=$
(2)在 Rt△ABC 中,∠C= 90°,若 a= 6,c= 10,则 b=

2. 方程思想的运用.
(1)如图 3-5,在△ABC 中,∠B= 90°,若 AB= x,BC= 4,AC= 8-x,则 AB=
(2)在 Rt△ABC 中,∠C= 90°,c= 34,a:b= 8:15,则 a=
思考:根据勾股定理,已知直角三角形两边可以求第三边,但在第(1)题中,只有一个已知量,为什么也能求得相应的边长?
1. 数形结合思想的运用.
(1)如图 3-4,在△ABC 中,∠B= 90°,一直角边为 a,斜边为 b,则另一直角边 c 满足$c^{2}=$
b² - a²
.(2)在 Rt△ABC 中,∠C= 90°,若 a= 6,c= 10,则 b=
8
;若 b= 3,∠A= 30°,则$a^{2}=$3
.

2. 方程思想的运用.
(1)如图 3-5,在△ABC 中,∠B= 90°,若 AB= x,BC= 4,AC= 8-x,则 AB=
3
,AC=5
.(2)在 Rt△ABC 中,∠C= 90°,c= 34,a:b= 8:15,则 a=
16
,b=30
.思考:根据勾股定理,已知直角三角形两边可以求第三边,但在第(1)题中,只有一个已知量,为什么也能求得相应的边长?
两个未知边用含同一未知数的代数式表示,可通过勾股定理列方程求解.
答案:1. (1) b² - a²;(2) 8;3
2. (1) 3;5;(2) 16;30
思考:两个未知边用含同一未知数的代数式表示,可通过勾股定理列方程求解.
3. (1) 3和4可能都是直角边或4为斜边,第三边可能为5或√7;(2) 126或66
2. (1) 3;5;(2) 16;30
思考:两个未知边用含同一未知数的代数式表示,可通过勾股定理列方程求解.
3. (1) 3和4可能都是直角边或4为斜边,第三边可能为5或√7;(2) 126或66
解析:
1. 数形结合思想的运用.
(1) 在Rt△ABC中,∠B=90°,由勾股定理得a²+c²=b²,故c²=b²-a².
(2) ∠C=90°,a=6,c=10,b²=c²-a²=10²-6²=64,b=8;∠A=30°,则斜边c=2a,由勾股定理a²+b²=c²,b=3,得a²+3²=(2a)²,解得a²=3.
2. 方程思想的运用.
(1) ∠B=90°,AB=x,BC=4,AC=8-x,由勾股定理x²+4²=(8-x)²,解得x=3,故AB=3,AC=5.
(2) ∠C=90°,a:b=8:15,设a=8k,b=15k,c=34,由勾股定理(8k)²+(15k)²=34²,解得k=2,故a=16,b=30.
思考:两个未知边用含同一未知数的代数式表示,可通过勾股定理列方程求解.
3. 分类讨论思想的运用.
(1) 3和4可能都是直角边(第三边5),或4为斜边、3为直角边(第三边√7),小明未分类讨论.
(2) 高AD在△ABC内部时,BD=16,DC=5,BC=21,面积=21×12/2=126;高AD在外部时,BC=16-5=11,面积=11×12/2=66.
(1) 在Rt△ABC中,∠B=90°,由勾股定理得a²+c²=b²,故c²=b²-a².
(2) ∠C=90°,a=6,c=10,b²=c²-a²=10²-6²=64,b=8;∠A=30°,则斜边c=2a,由勾股定理a²+b²=c²,b=3,得a²+3²=(2a)²,解得a²=3.
2. 方程思想的运用.
(1) ∠B=90°,AB=x,BC=4,AC=8-x,由勾股定理x²+4²=(8-x)²,解得x=3,故AB=3,AC=5.
(2) ∠C=90°,a:b=8:15,设a=8k,b=15k,c=34,由勾股定理(8k)²+(15k)²=34²,解得k=2,故a=16,b=30.
思考:两个未知边用含同一未知数的代数式表示,可通过勾股定理列方程求解.
3. 分类讨论思想的运用.
(1) 3和4可能都是直角边(第三边5),或4为斜边、3为直角边(第三边√7),小明未分类讨论.
(2) 高AD在△ABC内部时,BD=16,DC=5,BC=21,面积=21×12/2=126;高AD在外部时,BC=16-5=11,面积=11×12/2=66.