活动二:想一想 选一选
下列各组线段中不能组成直角三角形的是(
A.a= 8,b= 15,c= 17
B.a= 9,b= 12,c= 15
C.a= 6,b= 8,c= 10
D.a:b:c= 2:3:4
下列各组线段中不能组成直角三角形的是(
D
)A.a= 8,b= 15,c= 17
B.a= 9,b= 12,c= 15
C.a= 6,b= 8,c= 10
D.a:b:c= 2:3:4
答案:D
解析:
对于选项A:
$a=8, b=15, c=17$,
$a^{2} + b^{2} = 8^{2} + 15^{2} = 64 + 225 = 289$,
$c^{2} = 17^{2} = 289$,
因为 $a^{2} + b^{2} = c^{2}$,所以能组成直角三角形。
对于选项B:
$a=9, b=12, c=15$,
$a^{2} + b^{2} = 9^{2} + 12^{2} = 81 + 144 = 225$,
$c^{2} = 15^{2} = 225$,
因为 $a^{2} + b^{2} = c^{2}$,所以能组成直角三角形。
对于选项C:
$a=6, b=8, c=10$,
$a^{2} + b^{2} = 6^{2} + 8^{2} = 36 + 64 = 100$,
$c^{2} = 10^{2} = 100$,
因为 $a^{2} + b^{2} = c^{2}$,所以能组成直角三角形。
对于选项D:
设 $a=2x, b=3x, c=4x$,
$a^{2} + b^{2} = (2x)^{2} + (3x)^{2} = 4x^{2} + 9x^{2} = 13x^{2}$,
$c^{2} = (4x)^{2} = 16x^{2}$,
因为 $a^{2} + b^{2} \neq c^{2}$,所以不能组成直角三角形。
$a=8, b=15, c=17$,
$a^{2} + b^{2} = 8^{2} + 15^{2} = 64 + 225 = 289$,
$c^{2} = 17^{2} = 289$,
因为 $a^{2} + b^{2} = c^{2}$,所以能组成直角三角形。
对于选项B:
$a=9, b=12, c=15$,
$a^{2} + b^{2} = 9^{2} + 12^{2} = 81 + 144 = 225$,
$c^{2} = 15^{2} = 225$,
因为 $a^{2} + b^{2} = c^{2}$,所以能组成直角三角形。
对于选项C:
$a=6, b=8, c=10$,
$a^{2} + b^{2} = 6^{2} + 8^{2} = 36 + 64 = 100$,
$c^{2} = 10^{2} = 100$,
因为 $a^{2} + b^{2} = c^{2}$,所以能组成直角三角形。
对于选项D:
设 $a=2x, b=3x, c=4x$,
$a^{2} + b^{2} = (2x)^{2} + (3x)^{2} = 4x^{2} + 9x^{2} = 13x^{2}$,
$c^{2} = (4x)^{2} = 16x^{2}$,
因为 $a^{2} + b^{2} \neq c^{2}$,所以不能组成直角三角形。
活动三:算一算 写一写
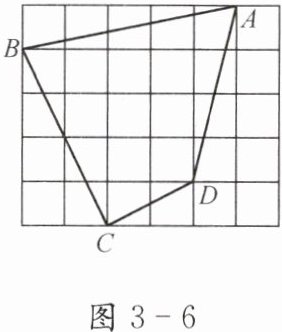
如图 3-6,每个小正方形的边长为 1.
(1)求四边形 ABCD 的面积;
(2)连接 BD,判断△BCD 的形状.
如图 3-6,每个小正方形的边长为 1.
(1)求四边形 ABCD 的面积;
(2)连接 BD,判断△BCD 的形状.

答案:(1)9;(2)直角三角形
解析:
(1) 采用割补法,以四边形ABCD各顶点的最左、最右、最上、最下位置确定一个长为4、宽为4的矩形,面积为4×4=16。减去周围四个直角三角形的面积:左上角三角形面积1/2×4×1=2,右上角三角形面积1/2×1×3=1.5,右下角三角形面积1/2×2×1=1,左下角三角形面积1/2×1×3=1.5。四边形ABCD面积=16-(2+1.5+1+1.5)=9。
(2) 连接BD,由勾股定理得:BC²=1²+3²=10,CD²=3²+1²=10,BD²=4²+2²=20。因为BC²+CD²=BD²,所以△BCD是直角三角形。
(2) 连接BD,由勾股定理得:BC²=1²+3²=10,CD²=3²+1²=10,BD²=4²+2²=20。因为BC²+CD²=BD²,所以△BCD是直角三角形。
1. 下列各组数中,不能作为直角三角形三边长的是(
A.9,16,25
B.$\sqrt{2}$,$\sqrt{2}$,2
C.6,8,10
D.5,12,13
A
)A.9,16,25
B.$\sqrt{2}$,$\sqrt{2}$,2
C.6,8,10
D.5,12,13
答案:A
解析:
对于选项A:
我们验证 $9^{2} + 16^{2}$ 是否等于 $25^{2}$。
计算得 $9^{2} + 16^{2} = 81 + 256 = 337$,
而 $25^{2} = 625$。
因为 $337 \neq 625$,所以A组不能构成直角三角形。
对于选项B:
我们验证 $(\sqrt{2})^{2} + (\sqrt{2})^{2}$ 是否等于 $2^{2}$。
计算得 $(\sqrt{2})^{2} + (\sqrt{2})^{2} = 2 + 2 = 4$,
而 $2^{2} = 4$。
因为 $4 = 4$,所以B组能构成直角三角形。
对于选项C:
我们验证 $6^{2} + 8^{2}$ 是否等于 $10^{2}$。
计算得 $6^{2} + 8^{2} = 36 + 64 = 100$,
而 $10^{2} = 100$。
因为 $100 = 100$,所以C组能构成直角三角形。
对于选项D:
我们验证 $5^{2} + 12^{2}$ 是否等于 $13^{2}$。
计算得 $5^{2} + 12^{2} = 25 + 144 = 169$,
而 $13^{2} = 169$。
因为 $169 = 169$,所以D组能构成直角三角形。
综上所述,只有A组不能构成直角三角形。
我们验证 $9^{2} + 16^{2}$ 是否等于 $25^{2}$。
计算得 $9^{2} + 16^{2} = 81 + 256 = 337$,
而 $25^{2} = 625$。
因为 $337 \neq 625$,所以A组不能构成直角三角形。
对于选项B:
我们验证 $(\sqrt{2})^{2} + (\sqrt{2})^{2}$ 是否等于 $2^{2}$。
计算得 $(\sqrt{2})^{2} + (\sqrt{2})^{2} = 2 + 2 = 4$,
而 $2^{2} = 4$。
因为 $4 = 4$,所以B组能构成直角三角形。
对于选项C:
我们验证 $6^{2} + 8^{2}$ 是否等于 $10^{2}$。
计算得 $6^{2} + 8^{2} = 36 + 64 = 100$,
而 $10^{2} = 100$。
因为 $100 = 100$,所以C组能构成直角三角形。
对于选项D:
我们验证 $5^{2} + 12^{2}$ 是否等于 $13^{2}$。
计算得 $5^{2} + 12^{2} = 25 + 144 = 169$,
而 $13^{2} = 169$。
因为 $169 = 169$,所以D组能构成直角三角形。
综上所述,只有A组不能构成直角三角形。
2. 填空题:
(1)若直角三角形的两边长分别为 5 和 12,则第三边长是
(2)请写出未完成的勾股数:9,40,
(1)若直角三角形的两边长分别为 5 和 12,则第三边长是
13或√119
.(2)请写出未完成的勾股数:9,40,
41
;8,15
,17.答案:(1) $13$或$\sqrt{119}$
(2) $41$ ; $15$
(2) $41$ ; $15$
解析:
(1)
当$12$是斜边时,第三边长是:
$\sqrt{12^{2} - 5^{2}} = \sqrt{144 - 25} = \sqrt{119}$,
当两直角边为$5$和$12$时,斜边为:
$\sqrt{12^{2} + 5^{2}} = \sqrt{144 + 25} = 13$,
综上所述,答案为:$13$或$\sqrt{119}$。
(2)
对于勾股数$9, 40, \underline{\hspace{1em}}$,设第三边为$c$,根据勾股定理有:
$c = \sqrt{9^{2} + 40^{2}} = \sqrt{81 + 1600} = \sqrt{1681} = 41$,
对于勾股数$8, \underline{\hspace{1em}}, 17$,设中间数为$b$,根据勾股定理有:
$b = \sqrt{17^{2} - 8^{2}} = \sqrt{289 - 64} = \sqrt{225} = 15$,
综上所述,答案为$41$ ; $15$。
当$12$是斜边时,第三边长是:
$\sqrt{12^{2} - 5^{2}} = \sqrt{144 - 25} = \sqrt{119}$,
当两直角边为$5$和$12$时,斜边为:
$\sqrt{12^{2} + 5^{2}} = \sqrt{144 + 25} = 13$,
综上所述,答案为:$13$或$\sqrt{119}$。
(2)
对于勾股数$9, 40, \underline{\hspace{1em}}$,设第三边为$c$,根据勾股定理有:
$c = \sqrt{9^{2} + 40^{2}} = \sqrt{81 + 1600} = \sqrt{1681} = 41$,
对于勾股数$8, \underline{\hspace{1em}}, 17$,设中间数为$b$,根据勾股定理有:
$b = \sqrt{17^{2} - 8^{2}} = \sqrt{289 - 64} = \sqrt{225} = 15$,
综上所述,答案为$41$ ; $15$。
3. 如图,在钝角三角形 ABC 中,CB= 9,AB= 17,AC= 10,AD⊥BC,垂足为 D. 求 CD 的长.


答案:设CD的长为x。
因为AD⊥BC,所以△ADC和△ADB均为直角三角形。
由于△ABC是钝角三角形,且AD为高,可知D在BC的延长线上(若D在BC上,则会出现负数解,舍去),则BD=BC+CD=9+x。
在Rt△ADC中,AD²=AC²-CD²=10²-x²=100-x²。
在Rt△ADB中,AD²=AB²-BD²=17²-(9+x)²=289-(81+18x+x²)=208-18x-x²。
因为AD²相等,所以100-x²=208-18x-x²,
化简得18x=108,解得x=6。
CD的长为6。
因为AD⊥BC,所以△ADC和△ADB均为直角三角形。
由于△ABC是钝角三角形,且AD为高,可知D在BC的延长线上(若D在BC上,则会出现负数解,舍去),则BD=BC+CD=9+x。
在Rt△ADC中,AD²=AC²-CD²=10²-x²=100-x²。
在Rt△ADB中,AD²=AB²-BD²=17²-(9+x)²=289-(81+18x+x²)=208-18x-x²。
因为AD²相等,所以100-x²=208-18x-x²,
化简得18x=108,解得x=6。
CD的长为6。
4. 如图,一架长 10 m 的梯子 AB 斜靠在墙上,梯子顶端到地面的垂直距离为 8 m. 如果梯子顶端下滑 2 m,那么它的底端是否也滑动 2 m?请说明理由.


答案:在$Rt\triangle ABC$中,$AB = 10m$,$AC = 8m$,根据勾股定理$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-8^{2}} = 6m$。
当梯子顶端下滑$2m$后,$AC' = 8 - 2 = 6m$。
在$Rt\triangle AB'C'$中,$AB' = 10m$,$AC' = 6m$,根据勾股定理$BC'=\sqrt{AB'^{2}-AC'^{2}}=\sqrt{10^{2}-6^{2}} = 8m$。
$BB' = BC' - BC = 8 - 6 = 2m$。
所以它的底端滑动$2m$。
当梯子顶端下滑$2m$后,$AC' = 8 - 2 = 6m$。
在$Rt\triangle AB'C'$中,$AB' = 10m$,$AC' = 6m$,根据勾股定理$BC'=\sqrt{AB'^{2}-AC'^{2}}=\sqrt{10^{2}-6^{2}} = 8m$。
$BB' = BC' - BC = 8 - 6 = 2m$。
所以它的底端滑动$2m$。