1. 如图,折叠直角三角形纸片 ABC,使点 C 落在 AB 上的点 E 处. 已知 BC= 12 cm,∠B= 30°,则 DE 的长是(
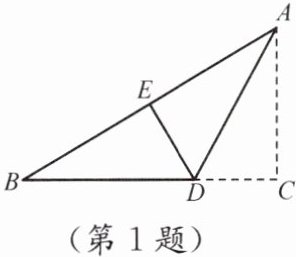
A.6 cm
B.4 cm
C.3 cm
D.2 cm
B
)
A.6 cm
B.4 cm
C.3 cm
D.2 cm
答案:B
解析:
设DE=x,由折叠性质得DC=DE=x,BD=BC-DC=12-x。
∵折叠后点C与E重合,∴∠C=∠DEB=90°(∠C为直角)。
在Rt△DEB中,∠B=30°,∴DE=1/2BD(30°角所对直角边是斜边一半)。
即x=1/2(12-x),解得x=4。
∵折叠后点C与E重合,∴∠C=∠DEB=90°(∠C为直角)。
在Rt△DEB中,∠B=30°,∴DE=1/2BD(30°角所对直角边是斜边一半)。
即x=1/2(12-x),解得x=4。
2. 如图,小明爸爸在鱼池边开了一块四边形土地,种了一些蔬菜. 爸爸让小明计算这块土地的面积,以便估算产量. 小明测得 AB= 4 m,BC= 3 m,CD= 13 m,DA= 12 m,又测得∠B= 90°. 求这块土地的面积.


答案:连接AC。
在Rt△ABC中,∠B=90°,AB=4m,BC=3m,
由勾股定理得:AC²=AB²+BC²=4²+3²=25,∴AC=5m。
S△ABC=1/2×AB×BC=1/2×4×3=6m²。
在△ADC中,AD=12m,AC=5m,CD=13m,
∵5²+12²=13²,即AC²+AD²=CD²,
∴△ADC是直角三角形,∠DAC=90°。
S△ADC=1/2×AC×AD=1/2×5×12=30m²。
四边形ABCD面积=S△ABC+S△ADC=6+30=36m²。
答:这块土地的面积为36m²。
在Rt△ABC中,∠B=90°,AB=4m,BC=3m,
由勾股定理得:AC²=AB²+BC²=4²+3²=25,∴AC=5m。
S△ABC=1/2×AB×BC=1/2×4×3=6m²。
在△ADC中,AD=12m,AC=5m,CD=13m,
∵5²+12²=13²,即AC²+AD²=CD²,
∴△ADC是直角三角形,∠DAC=90°。
S△ADC=1/2×AC×AD=1/2×5×12=30m²。
四边形ABCD面积=S△ABC+S△ADC=6+30=36m²。
答:这块土地的面积为36m²。
3. 问题:如图①,在等边三角形 ABC 内有一点 P,且$PA^{2}= 4$,$PB^{2}= 3$,$PC^{2}= 1$. 求∠BPC 的度数.
李明同学的思路:将△BPC 绕点 B 按逆时针方向旋转 60°,画出旋转后的图形(图②). 连接 PP',可得△P'PB 是等边三角形(可证),而△PP'A 又是直角三角形(由勾股定理的逆定理可证),从而可求出∠BPC 的度数.
请你写出李明同学求∠BPC 度数的完整过程.

李明同学的思路:将△BPC 绕点 B 按逆时针方向旋转 60°,画出旋转后的图形(图②). 连接 PP',可得△P'PB 是等边三角形(可证),而△PP'A 又是直角三角形(由勾股定理的逆定理可证),从而可求出∠BPC 的度数.
请你写出李明同学求∠BPC 度数的完整过程.

答案:将△BPC绕点B按逆时针方向旋转60°,得到△BP'A,连接PP'。
由旋转性质得:BP'=BP,P'A=PC,∠PBP'=60°,∠BP'A=∠BPC。
∵BP'=BP,∠PBP'=60°,∴△P'PB是等边三角形,∴PP'=BP,∠PP'B=60°。
∵PB²=3,∴PP'²=PB²=3。
∵PC²=1,∴P'A²=PC²=1。
∵PA²=4,∴P'A²+PP'²=1+3=4=PA²,由勾股定理逆定理得△PP'A是直角三角形,∠PP'A=90°。
∵△P'PB是等边三角形,∴∠PP'B=60°,∴∠BP'A=∠PP'B+∠PP'A=60°+90°=150°。
∵∠BP'A=∠BPC,∴∠BPC=150°。
答:∠BPC的度数为150°。
由旋转性质得:BP'=BP,P'A=PC,∠PBP'=60°,∠BP'A=∠BPC。
∵BP'=BP,∠PBP'=60°,∴△P'PB是等边三角形,∴PP'=BP,∠PP'B=60°。
∵PB²=3,∴PP'²=PB²=3。
∵PC²=1,∴P'A²=PC²=1。
∵PA²=4,∴P'A²+PP'²=1+3=4=PA²,由勾股定理逆定理得△PP'A是直角三角形,∠PP'A=90°。
∵△P'PB是等边三角形,∴∠PP'B=60°,∴∠BP'A=∠PP'B+∠PP'A=60°+90°=150°。
∵∠BP'A=∠BPC,∴∠BPC=150°。
答:∠BPC的度数为150°。