2. 某校九年级(2)班的 10 名团员在献爱心捐款活动中,捐款情况如下(单位:元):10,8,12,15,10,12,11,9,13,10,这组数据的(
A.众数是 10.5
B.方差是 3.8
C.极差是 8
D.中位数是 10
B
)A.众数是 10.5
B.方差是 3.8
C.极差是 8
D.中位数是 10
答案:B
解析:
将数据从小到大排列:8,9,10,10,10,11,12,12,13,15.
众数:10出现3次,次数最多,众数为10.
中位数:第5、6个数分别为10、11,中位数为$\frac{10+11}{2}=10.5$.
极差:15-8=7.
平均数:$\frac{8+9+10+10+10+11+12+12+13+15}{10}=11$.
方差:$\frac{1}{10}[(8-11)^2+(9-11)^2+3×(10-11)^2+(11-11)^2+2×(12-11)^2+(13-11)^2+(15-11)^2]=\frac{1}{10}(9+4+3+0+2+4+16)=3.8$.
结论:方差是3.8,选B.
众数:10出现3次,次数最多,众数为10.
中位数:第5、6个数分别为10、11,中位数为$\frac{10+11}{2}=10.5$.
极差:15-8=7.
平均数:$\frac{8+9+10+10+10+11+12+12+13+15}{10}=11$.
方差:$\frac{1}{10}[(8-11)^2+(9-11)^2+3×(10-11)^2+(11-11)^2+2×(12-11)^2+(13-11)^2+(15-11)^2]=\frac{1}{10}(9+4+3+0+2+4+16)=3.8$.
结论:方差是3.8,选B.
3. 一枚质地均匀的正方体骰子的六个面分别标有数字 1,2,3,4,5,6,投掷这枚骰子 5 次,记录每次骰子向上一面的数字.下面的统计结果中,能判断记录的这 5 个数字中一定没有出现 6 的是(
A.中位数是 3,众数是 2
B.平均数是 3,中位数是 2
C.平均数是 3,方差是 2
D.平均数是 3,众数是 2
C
)A.中位数是 3,众数是 2
B.平均数是 3,中位数是 2
C.平均数是 3,方差是 2
D.平均数是 3,众数是 2
答案:C
解析:
选项A:中位数是3,众数是2
可能的5个数:2,2,3,4,6(含6),故A不符合。
选项B:平均数是3,中位数是2
设5个数从小到大:$a,b,2,d,e$,且$a+b+2+d+e=15$。
可能的数:1,1,2,5,6(含6),故B不符合。
选项C:平均数是3,方差是2
设5个数为$x_1,x_2,x_3,x_4,x_5$,则$\sum x_i=15$,方差$s^2=\frac{1}{5}\sum (x_i-3)^2=2$,即$\sum (x_i-3)^2=10$。
若含6,则$(6-3)^2=9$,剩余4个数需满足$\sum (x_i-3)^2=1$且$\sum x_i=9$。
剩余4个数只能为3,3,3,0(0不存在)或2,3,3,1($(2-3)^2+(1-3)^2=1+4=5>1$),矛盾。
故一定不含6,C符合。
选项D:平均数是3,众数是2
可能的5个数:2,2,2,3,6(含6),故D不符合。
答案:C
可能的5个数:2,2,3,4,6(含6),故A不符合。
选项B:平均数是3,中位数是2
设5个数从小到大:$a,b,2,d,e$,且$a+b+2+d+e=15$。
可能的数:1,1,2,5,6(含6),故B不符合。
选项C:平均数是3,方差是2
设5个数为$x_1,x_2,x_3,x_4,x_5$,则$\sum x_i=15$,方差$s^2=\frac{1}{5}\sum (x_i-3)^2=2$,即$\sum (x_i-3)^2=10$。
若含6,则$(6-3)^2=9$,剩余4个数需满足$\sum (x_i-3)^2=1$且$\sum x_i=9$。
剩余4个数只能为3,3,3,0(0不存在)或2,3,3,1($(2-3)^2+(1-3)^2=1+4=5>1$),矛盾。
故一定不含6,C符合。
选项D:平均数是3,众数是2
可能的5个数:2,2,2,3,6(含6),故D不符合。
答案:C
4. 某种蔬菜按品质分成三个等级销售,销售情况如下表:
|等级|单价|销售量|
|一等|5.0 元/kg|20 kg|
|二等|4.5 元/kg|40 kg|
|三等|4.0 元/kg|40 kg|
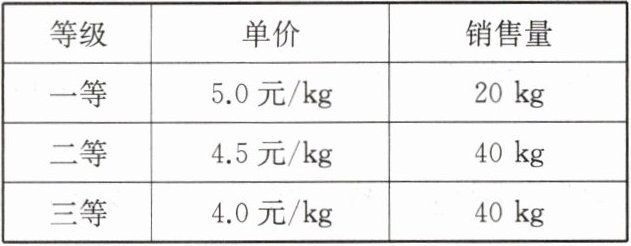
则售出蔬菜的平均单价为
|等级|单价|销售量|
|一等|5.0 元/kg|20 kg|
|二等|4.5 元/kg|40 kg|
|三等|4.0 元/kg|40 kg|

则售出蔬菜的平均单价为
4.4
元/kg.答案:4.4
解析:
总销售额为:$5.0×20 + 4.5×40 + 4.0×40 = 100 + 180 + 160 = 440$(元)
总销售量为:$20 + 40 + 40 = 100$(kg)
平均单价为:$\frac{440}{100} = 4.4$(元/kg)
4.4
总销售量为:$20 + 40 + 40 = 100$(kg)
平均单价为:$\frac{440}{100} = 4.4$(元/kg)
4.4
5. 某市 6 月份日平均气温统计如图所示,则在日平均气温这组数据中,众数为
21℃
,中位数为22℃
.答案:21℃
22℃
22℃
6. 已知样本数据$x_{1},x_{2},x_{3},x_{4},x_{5}$的方差为 8,那么另一组数据$x_{1}-2,x_{2}-2,x_{3}-2,x_{4}-2,x_{5}-2$的方差是______
8
.答案:8
7. 某公司销售部有营业员 15 人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,公司有关部门统计了这 15 人某月的销售量,如下表所示:
|月销售量/件|1770|480|220|180|120|90|
|人数/人|1|1|3|3|3|4|

(1)直接写出这 15 名营业员该月销售量数据的平均数、中位数、众数.
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标?请说明理由.
|月销售量/件|1770|480|220|180|120|90|
|人数/人|1|1|3|3|3|4|

(1)直接写出这 15 名营业员该月销售量数据的平均数、中位数、众数.
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标?请说明理由.
答案:解:(1)平均数:278,中位数:180,众数:90
.(2)如果想让一半左右的营业员都能达到销售目标平均数,中位数、众数中,
中位数最适合作为月销售目标. 理由如下:
如果以平均数278件作为月销售目标时,销售量大于278件的人数为2人,小于278件的人数
为13人,不符合题意.如果以中位数180件作为月销售目标时,月销售量大于等于180件的
人数为8人,小于180件的人数为7人,符合题意.如果以众数90件作为月销售目标时,
所有人都达到月销售目标,不符合题意.
∴中位数最适合作为月销售目标,有一半左右的营业员能达到销售目标.
.(2)如果想让一半左右的营业员都能达到销售目标平均数,中位数、众数中,
中位数最适合作为月销售目标. 理由如下:
如果以平均数278件作为月销售目标时,销售量大于278件的人数为2人,小于278件的人数
为13人,不符合题意.如果以中位数180件作为月销售目标时,月销售量大于等于180件的
人数为8人,小于180件的人数为7人,符合题意.如果以众数90件作为月销售目标时,
所有人都达到月销售目标,不符合题意.
∴中位数最适合作为月销售目标,有一半左右的营业员能达到销售目标.