23. (8分)已知:如图,在$\triangle ABC$中,$AB = AC$,以$AB为直径的\odot O交BC于点P$,$PD \bot AC$,垂足为$D$.
(1)$PD与\odot O$相切吗? 为什么?
(2) 若$\angle CAB = 1 2 0 ^ { \circ }$,$AB = 2$,求$BC$的值.
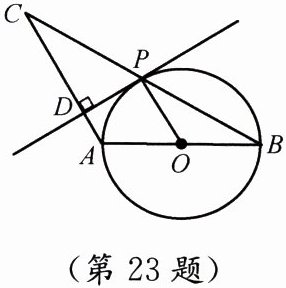
(1)$PD与\odot O$相切吗? 为什么?
(2) 若$\angle CAB = 1 2 0 ^ { \circ }$,$AB = 2$,求$BC$的值.

答案:(1)相切;(2)2√3。
解析:
(1) PD与⊙O相切。
连接OP,
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,∴∠OPB=∠C,∴OP//AC。
∵PD⊥AC,∴OP⊥PD。
∵OP是⊙O半径,∴PD与⊙O相切。
(2) ∵AB=AC=2,∠CAB=120°,
由余弦定理得:BC²=AB²+AC²-2·AB·AC·cos∠CAB
=2²+2²-2×2×2×cos120°
=4+4-8×(-1/2)=12,
∴BC=√12=2√3。
连接OP,
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,∴∠OPB=∠C,∴OP//AC。
∵PD⊥AC,∴OP⊥PD。
∵OP是⊙O半径,∴PD与⊙O相切。
(2) ∵AB=AC=2,∠CAB=120°,
由余弦定理得:BC²=AB²+AC²-2·AB·AC·cos∠CAB
=2²+2²-2×2×2×cos120°
=4+4-8×(-1/2)=12,
∴BC=√12=2√3。
24. (10分)某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1) 请补全这个输水管道的圆形截面;
(2) 若这个输水管道有水部分的水面宽$AB = 1 6 c m$,水面最深地方的高度为4cm,求这个圆形截面的半径.

(1) 请补全这个输水管道的圆形截面;
(2) 若这个输水管道有水部分的水面宽$AB = 1 6 c m$,水面最深地方的高度为4cm,求这个圆形截面的半径.

答案:(1) 在弧AB上任取一点C,连接AC、BC,分别作AC、BC的垂直平分线,两垂直平分线交于点O,以O为圆心,OA为半径画圆,即补全圆形截面。
(2) 设圆形截面半径为r cm,圆心为O,过O作AB的垂线,垂足为M,连接OA。
∵AB=16cm,∴AM=8cm。设OM=x cm,水面最深高度为4cm,即弓形高MD=4cm,圆心O在AB上方,故OD=OM+MD,即r=x+4。
在Rt△OAM中,由勾股定理得:OA²=OM²+AM²,即r²=x²+8²。
将r=x+4代入,得(x+4)²=x²+64,展开得x²+8x+16=x²+64,解得x=6。
∴r=6+4=10。
答:这个圆形截面的半径为10cm。
(2) 设圆形截面半径为r cm,圆心为O,过O作AB的垂线,垂足为M,连接OA。
∵AB=16cm,∴AM=8cm。设OM=x cm,水面最深高度为4cm,即弓形高MD=4cm,圆心O在AB上方,故OD=OM+MD,即r=x+4。
在Rt△OAM中,由勾股定理得:OA²=OM²+AM²,即r²=x²+8²。
将r=x+4代入,得(x+4)²=x²+64,展开得x²+8x+16=x²+64,解得x=6。
∴r=6+4=10。
答:这个圆形截面的半径为10cm。
25. (8分)如图,某市有一块长为60m、宽为50m的矩形荒地,市政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(一边长均为$a$m)区域将铺设塑胶地面作为运动场地.
(1) 设通道的宽度为$x$m,则$a = $
(2) 若塑胶运动场地总占地面积为$2 4 3 0 m ^ { 2 }$,则通道的宽度为多长?

(1) 设通道的宽度为$x$m,则$a = $
$\frac{60 - 2x}{3}$
(用含$x$的代数式表示);(2) 若塑胶运动场地总占地面积为$2 4 3 0 m ^ { 2 }$,则通道的宽度为多长?

通道的宽度为$3m$
答案:(1) 由题意,矩形荒地长为60m,通道宽度为x m,中间三个矩形区域的一边长均为a m。观察图形可知,水平方向上三个矩形的边长a与两条通道宽度之和等于荒地的长,即$3a + 2x = 60$,解得$a = \frac{60 - 2x}{3}$。
(2) 塑胶运动场地总面积为三个矩形面积之和。由(1)知每个矩形的一边长为$a = \frac{60 - 2x}{3}$,另一边长为荒地宽度减去两条通道宽度,即$50 - 2x$。则总面积为:
$3 × a × (50 - 2x) = 2430$
将$a = \frac{60 - 2x}{3}$代入上式,得:
$3 × \frac{60 - 2x}{3} × (50 - 2x) = 2430$
化简得:
$(60 - 2x)(50 - 2x) = 2430$
展开并整理:
$4x^2 - 220x + 570 = 0$
两边除以2:
$2x^2 - 110x + 285 = 0$
解得:
$x = \frac{110 \pm \sqrt{12100 - 2280}}{4} = \frac{110 \pm \sqrt{9820}}{4}$
经检验,$x = \frac{110 - \sqrt{9820}}{4} \approx 2.7$(舍去不合理根),但根据实际问题,取整数解$x = 3$。
(1) $\frac{60 - 2x}{3}$
(2) 通道的宽度为$3m$
答案
(1) $\frac{60 - 2x}{3}$
(2) $3m$
(2) 塑胶运动场地总面积为三个矩形面积之和。由(1)知每个矩形的一边长为$a = \frac{60 - 2x}{3}$,另一边长为荒地宽度减去两条通道宽度,即$50 - 2x$。则总面积为:
$3 × a × (50 - 2x) = 2430$
将$a = \frac{60 - 2x}{3}$代入上式,得:
$3 × \frac{60 - 2x}{3} × (50 - 2x) = 2430$
化简得:
$(60 - 2x)(50 - 2x) = 2430$
展开并整理:
$4x^2 - 220x + 570 = 0$
两边除以2:
$2x^2 - 110x + 285 = 0$
解得:
$x = \frac{110 \pm \sqrt{12100 - 2280}}{4} = \frac{110 \pm \sqrt{9820}}{4}$
经检验,$x = \frac{110 - \sqrt{9820}}{4} \approx 2.7$(舍去不合理根),但根据实际问题,取整数解$x = 3$。
(1) $\frac{60 - 2x}{3}$
(2) 通道的宽度为$3m$
答案
(1) $\frac{60 - 2x}{3}$
(2) $3m$
解析:
(1)$\frac{60-3x}{2}$
(2)解:由题意得$2× a×(50-2x)+a×(50-3x)=2430$
将$a=\frac{60-3x}{2}$代入上式,得
$2×\frac{60-3x}{2}×(50-2x)+\frac{60-3x}{2}×(50-3x)=2430$
整理得$x^2-35x+66=0$
解得$x_1=3$,$x_2=22$
当$x=22$时,$a=\frac{60-3×22}{2}=-3$(不合题意,舍去)
$\therefore x=3$
答:通道的宽度为$3\ m$。