26. (10分)已知关于$x的一元二次方程x ^ { 2 } - ( 2 k + 1 ) x + k ^ { 2 } + 2 k = 0有两个实数根x _ { 1 }$、$x _ { 2 }$.
(1) 求实数$k$的取值范围.
(2) 是否存在实数$k$,使得$x _ { 1 } \cdot x _ { 2 } - x _ { 1 } ^ { 2 } - x _ { 2 } ^ { 2 } \geqslant 0$成立? 若存在,求出$k$的值;若不存在,请说明理由.
(1) 求实数$k$的取值范围.
(2) 是否存在实数$k$,使得$x _ { 1 } \cdot x _ { 2 } - x _ { 1 } ^ { 2 } - x _ { 2 } ^ { 2 } \geqslant 0$成立? 若存在,求出$k$的值;若不存在,请说明理由.
答案:答题卡:
(1)
方程$x^{2} - (2k + 1)x + k^{2} + 2k = 0$有两个实数根,则判别式$\Delta\geqslant0$。
$\Delta =(2k + 1)^{2}-4(k^{2}+2k)=4k^{2}+4k + 1-4k^{2}-8k=1 - 4k\geqslant0$,
解得$k\leqslant\frac{1}{4}$。
(2)
由韦达定理可知$x_{1}+x_{2}=2k + 1$,$x_{1}x_{2}=k^{2}+2k$。
$x_{1}\cdot x_{2}-x_{1}^{2}-x_{2}^{2}=x_{1}x_{2}-(x_{1}^{2}+x_{2}^{2})=x_{1}x_{2}-[(x_{1}+x_{2})^{2}-2x_{1}x_{2}]=3x_{1}x_{2}-(x_{1}+x_{2})^{2}$
将$x_{1}+x_{2}=2k + 1$,$x_{1}x_{2}=k^{2}+2k$代入上式得:
$3(k^{2}+2k)-(2k + 1)^{2}=3k^{2}+6k-(4k^{2}+4k + 1)=3k^{2}+6k - 4k^{2}-4k - 1=-k^{2}+2k - 1$
若$x_{1}\cdot x_{2}-x_{1}^{2}-x_{2}^{2}\geqslant0$,则$-k^{2}+2k - 1\geqslant0$,即$k^{2}-2k + 1\leqslant0$,$(k - 1)^{2}\leqslant0$。
因为任何数的平方都大于等于$0$,所以$(k - 1)^{2}=0$,解得$k = 1$。
又因为由(1)知$k\leqslant\frac{1}{4}$,$1\gt\frac{1}{4}$,所以不存在实数$k$,使得$x_{1}\cdot x_{2}-x_{1}^{2}-x_{2}^{2}\geqslant0$成立。
综上,答案依次为:(1)$k\leqslant\frac{1}{4}$;(2)不存在,理由如上述。
(1)
方程$x^{2} - (2k + 1)x + k^{2} + 2k = 0$有两个实数根,则判别式$\Delta\geqslant0$。
$\Delta =(2k + 1)^{2}-4(k^{2}+2k)=4k^{2}+4k + 1-4k^{2}-8k=1 - 4k\geqslant0$,
解得$k\leqslant\frac{1}{4}$。
(2)
由韦达定理可知$x_{1}+x_{2}=2k + 1$,$x_{1}x_{2}=k^{2}+2k$。
$x_{1}\cdot x_{2}-x_{1}^{2}-x_{2}^{2}=x_{1}x_{2}-(x_{1}^{2}+x_{2}^{2})=x_{1}x_{2}-[(x_{1}+x_{2})^{2}-2x_{1}x_{2}]=3x_{1}x_{2}-(x_{1}+x_{2})^{2}$
将$x_{1}+x_{2}=2k + 1$,$x_{1}x_{2}=k^{2}+2k$代入上式得:
$3(k^{2}+2k)-(2k + 1)^{2}=3k^{2}+6k-(4k^{2}+4k + 1)=3k^{2}+6k - 4k^{2}-4k - 1=-k^{2}+2k - 1$
若$x_{1}\cdot x_{2}-x_{1}^{2}-x_{2}^{2}\geqslant0$,则$-k^{2}+2k - 1\geqslant0$,即$k^{2}-2k + 1\leqslant0$,$(k - 1)^{2}\leqslant0$。
因为任何数的平方都大于等于$0$,所以$(k - 1)^{2}=0$,解得$k = 1$。
又因为由(1)知$k\leqslant\frac{1}{4}$,$1\gt\frac{1}{4}$,所以不存在实数$k$,使得$x_{1}\cdot x_{2}-x_{1}^{2}-x_{2}^{2}\geqslant0$成立。
综上,答案依次为:(1)$k\leqslant\frac{1}{4}$;(2)不存在,理由如上述。
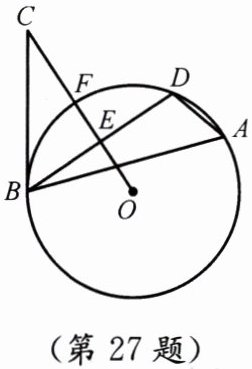
27. (12分)如图,$\triangle ABD是\odot O$的内接三角形,$E是弦BD$的中点,$C是\odot O$外一点,且$\angle DBC = \angle A = 6 0 ^ { \circ }$,连接$OE$,$OE的延长线与\odot O相交于点F$,与$BC相交于点C$.
(1) 求证:$BC是\odot O$的切线;
(2) 若$\odot O$的半径为6cm,求弦$BD$的长.
(1) 求证:$BC是\odot O$的切线;
(2) 若$\odot O$的半径为6cm,求弦$BD$的长.

答案:(1) 证明见上;(2) 6√3 cm。
解析:
(1) 连接OB。
∵E是弦BD的中点,∴OE⊥BD(垂径定理),∠OEB=90°。
∵∠A是圆周角,∠A=60°,∴弧BD所对的圆心角∠BOD=2∠A=120°(圆周角定理)。
∵OB=OD,E是BD中点,∴OE平分∠BOD(等腰三角形三线合一),∠BOE=∠BOD/2=60°。
在Rt△OEB中,∠OBE=90°-∠BOE=30°。
∵∠DBC=60°,∴∠OBC=∠OBE+∠DBC=30°+60°=90°,即OB⊥BC。
∵OB是⊙O半径,∴BC是⊙O的切线。
(2) 在Rt△OEB中,OB=6cm,∠BOE=60°,
∴sin∠BOE=BE/OB,BE=OB·sin60°=6×(√3/2)=3√3 cm。
∵E是BD中点,∴BD=2BE=2×3√3=6√3 cm。
∵E是弦BD的中点,∴OE⊥BD(垂径定理),∠OEB=90°。
∵∠A是圆周角,∠A=60°,∴弧BD所对的圆心角∠BOD=2∠A=120°(圆周角定理)。
∵OB=OD,E是BD中点,∴OE平分∠BOD(等腰三角形三线合一),∠BOE=∠BOD/2=60°。
在Rt△OEB中,∠OBE=90°-∠BOE=30°。
∵∠DBC=60°,∴∠OBC=∠OBE+∠DBC=30°+60°=90°,即OB⊥BC。
∵OB是⊙O半径,∴BC是⊙O的切线。
(2) 在Rt△OEB中,OB=6cm,∠BOE=60°,
∴sin∠BOE=BE/OB,BE=OB·sin60°=6×(√3/2)=3√3 cm。
∵E是BD中点,∴BD=2BE=2×3√3=6√3 cm。