1. 对甲、乙两名同学100m短跑进行5次测试,通过计算,他们成绩的平均数相等,方差$s^{2}_{甲}= 0.025$,$s^{2}_{乙}= 0.246$.下列说法中,正确的是(
A.甲短跑成绩比乙好
B.乙短跑成绩比甲好
C.甲短跑成绩比乙稳定
D.乙短跑成绩比甲稳定
C
)A.甲短跑成绩比乙好
B.乙短跑成绩比甲好
C.甲短跑成绩比乙稳定
D.乙短跑成绩比甲稳定
答案:C
解析:
方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定。已知$s^{2}_{甲}= 0.025$,$s^{2}_{乙}= 0.246$,因为$0.025\lt0.246$,即$s^{2}_{甲}\lt s^{2}_{乙}$,所以甲的成绩比乙的成绩稳定。
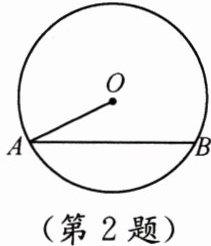
2. 如图,已知$\odot O$的半径为13,弦$AB$长为24,则点$O到AB$的距离是(
A.3
B.4
C.5
D.6
C
)
A.3
B.4
C.5
D.6
答案:C
解析:
作$OC\perp AB$于$C$点,根据垂径定理,垂直于弦的直径平分弦,所以$AC = \frac{1}{2}AB=\frac{1}{2}×24 = 12$。
在$Rt\triangle AOC$中,$OA = 13$,$AC = 12$,根据勾股定理$OC=\sqrt{OA^{2}-AC^{2}}=\sqrt{13^{2}-12^{2}}=\sqrt{169 - 144}=\sqrt{25}=5$。
即点$O$到$AB$的距离是$5$。
在$Rt\triangle AOC$中,$OA = 13$,$AC = 12$,根据勾股定理$OC=\sqrt{OA^{2}-AC^{2}}=\sqrt{13^{2}-12^{2}}=\sqrt{169 - 144}=\sqrt{25}=5$。
即点$O$到$AB$的距离是$5$。
3. 某超市1月份的营业额为36万元,3月份的营业额为48万元,设每月营业额的平均增长率为$x$,则可列方程为(
A.$48(1 - x)^{2}= 36$
B.$48(1 + x)^{2}= 36$
C.$36(1 - x)^{2}= 48$
D.$36(1 + x)^{2}= 48$
D
)A.$48(1 - x)^{2}= 36$
B.$48(1 + x)^{2}= 36$
C.$36(1 - x)^{2}= 48$
D.$36(1 + x)^{2}= 48$
答案:D
解析:
设每月的平均增长率为$x$,那么2月份的营业额为$36(1 + x)$万元。
3月份的营业额为$36(1 + x)^2$万元。
根据题意,3月份的营业额为48万元,因此方程为:
$36(1 + x)^2 = 48$
3月份的营业额为$36(1 + x)^2$万元。
根据题意,3月份的营业额为48万元,因此方程为:
$36(1 + x)^2 = 48$
4. 已知圆锥的底面半径为3cm,高为4cm,则它的侧面积为(
A.$15\pi cm^{2}$
B.$16\pi cm^{2}$
C.$19\pi cm^{2}$
D.$24\pi cm^{2}$
A
)A.$15\pi cm^{2}$
B.$16\pi cm^{2}$
C.$19\pi cm^{2}$
D.$24\pi cm^{2}$
答案:A
解析:
圆锥的底面半径$r = 3cm$,根据圆锥底面周长公式$C = 2\pi r$,可得底面周长$C = 2\pi×3 = 6\picm$。
圆锥的高$h = 4cm$,由勾股定理求母线长$l$,$l=\sqrt{r^{2}+h^{2}}=\sqrt{3^{2}+4^{2}} = 5cm$。
根据圆锥侧面积公式$S=\frac{1}{2}Cl$,把$C = 6\picm$,$l = 5cm$代入可得$S=\frac{1}{2}×6\pi×5 = 15\picm^{2}$。
圆锥的高$h = 4cm$,由勾股定理求母线长$l$,$l=\sqrt{r^{2}+h^{2}}=\sqrt{3^{2}+4^{2}} = 5cm$。
根据圆锥侧面积公式$S=\frac{1}{2}Cl$,把$C = 6\picm$,$l = 5cm$代入可得$S=\frac{1}{2}×6\pi×5 = 15\picm^{2}$。
5. 一元二次方程$2x^{2}-7x - 15 = 0$的根的情况是(
A.有两个正的实数根
B.有两个负的实数根
C.两根的符号相反
D.方程没有实数根
C
)A.有两个正的实数根
B.有两个负的实数根
C.两根的符号相反
D.方程没有实数根
答案:C
解析:
对于一元二次方程 $2x^{2}-7x - 15 = 0$,这里 $a = 2$,$b = -7$,$c = -15$,判别式 $\Delta=b^{2}-4ac=(-7)^{2}-4×2×(-15)=49 + 120 = 169\gt0$,所以方程有两个实数根。
根据韦达定理,两根之积 $x_1x_2=\frac{c}{a}=\frac{-15}{2}\lt0$,所以两根符号相反。
根据韦达定理,两根之积 $x_1x_2=\frac{c}{a}=\frac{-15}{2}\lt0$,所以两根符号相反。
6. 根据下列表格中的对应值:
| $x$ | $3.23$ | $3.24$ | $3.25$ | $3.26$ |
| $ax^{2}+bx + c$ | $-0.06$ | $-0.02$ | $0.03$ | $0.09$ |

判断方程$ax^{2}+bx + c = 0(a\neq0,a、b、c$为常数)的一个解$x$的范围是(
A.$3.22\lt x\lt3.23$
B.$3.23\lt x\lt3.24$
C.$3.24\lt x\lt3.25$
D.$3.25\lt x\lt3.26$
| $x$ | $3.23$ | $3.24$ | $3.25$ | $3.26$ |
| $ax^{2}+bx + c$ | $-0.06$ | $-0.02$ | $0.03$ | $0.09$ |

判断方程$ax^{2}+bx + c = 0(a\neq0,a、b、c$为常数)的一个解$x$的范围是(
C
)A.$3.22\lt x\lt3.23$
B.$3.23\lt x\lt3.24$
C.$3.24\lt x\lt3.25$
D.$3.25\lt x\lt3.26$
答案:C
解析:
根据表格可知,当$x = 3.24$时,$ax^{2}+bx + c=-0.02\lt0$;当$x = 3.25$时,$ax^{2}+bx + c = 0.03\gt0$。
因为二次函数$y = ax^{2}+bx + c$的图象是连续的,所以在$3.24$到$3.25$之间一定会经过$y = 0$这个点,即方程$ax^{2}+bx + c = 0$的一个解$x$的范围是$3.24\lt x\lt3.25$。
因为二次函数$y = ax^{2}+bx + c$的图象是连续的,所以在$3.24$到$3.25$之间一定会经过$y = 0$这个点,即方程$ax^{2}+bx + c = 0$的一个解$x$的范围是$3.24\lt x\lt3.25$。
7. 一只不透明的袋子中装有红球、黑球、白球若干个,这些球除颜色外都相同,小新从袋中随机摸出1球,记下颜色后放回,摇匀后再摸出1球,记下颜色,如此经过大量摸球试验后,小新发现其中摸出红球的频率稳定在20%,摸出黑球的频率稳定在50%.对此试验,他总结出下列结论:① 若进行大量摸球试验,摸出白球的频率稳定在30%,② 从袋中任意摸出1球,该球是黑球的概率最大;③ 若再摸球100次,必有20次摸出的是红球.其中,说法正确的是(
A.①②③
B.①②
C.①③
D.②③
B
)A.①②③
B.①②
C.①③
D.②③
答案:B
解析:
1. 根据题意,红球的频率稳定在20%,黑球的频率稳定在50%,因此白球的频率为$1 - 20\% - 50\% = 30\%$,故①正确。
2. 黑球的频率最高(50%),因此从袋中任意摸出1球,该球是黑球的概率最大,故②正确。
3. 频率稳定不代表每次试验都严格对应比例,若再摸球100次,不一定恰有20次摸出红球,故③错误。
2. 黑球的频率最高(50%),因此从袋中任意摸出1球,该球是黑球的概率最大,故②正确。
3. 频率稳定不代表每次试验都严格对应比例,若再摸球100次,不一定恰有20次摸出红球,故③错误。