8. 有5张卡片(形状、大小、质地都相同),正面分别画有下列图形:① 线段;② 正三角形;③ 平行四边形;④ 等腰梯形;⑤ 圆.将卡片背面朝上洗匀,从中抽取1张,正面图形一定满足既是轴对称图形,又是中心对称图形的概率是(
A.$\frac{1}{5}$
B.$\frac{2}{5}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
B
)A.$\frac{1}{5}$
B.$\frac{2}{5}$
C.$\frac{3}{5}$
D.$\frac{4}{5}$
答案:B
解析:
首先,需要明确哪些图形既是轴对称图形又是中心对称图形。
①线段:既是轴对称图形,又是中心对称图形。
②正三角形:只是轴对称图形,不是中心对称图形。
③平行四边形:不一定是轴对称图形(除非它是特殊平行四边形,如正方形或矩形),但如果是一般的平行四边形,则它只是中心对称图形,不是轴对称图形,题目没有指明,所以按一般情况处理。
④等腰梯形:只是轴对称图形,不是中心对称图形。
⑤圆:既是轴对称图形,又是中心对称图形。
因此,从5张卡片中,满足条件的图形有2个(线段和圆)。
所以,从中抽取1张,正面图形一定满足既是轴对称图形,又是中心对称图形的概率是 $\frac{2}{5}$。
①线段:既是轴对称图形,又是中心对称图形。
②正三角形:只是轴对称图形,不是中心对称图形。
③平行四边形:不一定是轴对称图形(除非它是特殊平行四边形,如正方形或矩形),但如果是一般的平行四边形,则它只是中心对称图形,不是轴对称图形,题目没有指明,所以按一般情况处理。
④等腰梯形:只是轴对称图形,不是中心对称图形。
⑤圆:既是轴对称图形,又是中心对称图形。
因此,从5张卡片中,满足条件的图形有2个(线段和圆)。
所以,从中抽取1张,正面图形一定满足既是轴对称图形,又是中心对称图形的概率是 $\frac{2}{5}$。
9. 一组数据$-2,-1,0,x,1$的平均数是0,方差$s^{2}=$
2
.答案:2
解析:
已知数据$-2, -1, 0, x, 1$的平均数为0,根据平均数公式:
$\frac{-2 + (-1) + 0 + x + 1}{5} = 0$,
化简得:
$-2 -1 + 0 + x + 1 = 0$,
解得:
$x = 2$。
现在,已知数据为$-2, -1, 0, 2, 1$,根据方差公式:
$s^{2} = \frac{1}{n}\sum_{i=1}^{n}(x_{i} - \bar{x})^{2}$,
其中,$n = 5$,平均数$\bar{x} = 0$,代入公式得:
$s^{2} = \frac{1}{5}[(-2 - 0)^{2} + (-1 - 0)^{2} + (0 - 0)^{2} + (2 - 0)^{2} + (1 - 0)^{2}]$
$ = \frac{1}{5}[4 + 1 + 0 + 4 + 1]$
$ = \frac{1}{5} × 10$
$ = 2$
$\frac{-2 + (-1) + 0 + x + 1}{5} = 0$,
化简得:
$-2 -1 + 0 + x + 1 = 0$,
解得:
$x = 2$。
现在,已知数据为$-2, -1, 0, 2, 1$,根据方差公式:
$s^{2} = \frac{1}{n}\sum_{i=1}^{n}(x_{i} - \bar{x})^{2}$,
其中,$n = 5$,平均数$\bar{x} = 0$,代入公式得:
$s^{2} = \frac{1}{5}[(-2 - 0)^{2} + (-1 - 0)^{2} + (0 - 0)^{2} + (2 - 0)^{2} + (1 - 0)^{2}]$
$ = \frac{1}{5}[4 + 1 + 0 + 4 + 1]$
$ = \frac{1}{5} × 10$
$ = 2$
10. 一组数据3,6,$-1,4,2$的中位数是
3
.答案:3
解析:
首先将数据按从小到大的顺序重新排列:$-1, 2, 3, 4, 6$。数据共有5个数,为奇数个,中位数为中间的数,即第3个数,因此中位数是3。
11. 若关于$x的一元二次方程kx^{2}-(2k + 1)x + k = 0$有两个不相等的实数根,则$k$的取值范围是
$k> -\frac{1}{4}$且$k \neq 0$
.答案:$k> -\frac{1}{4}$且$k \neq 0$
解析:
由题意,方程 $k x^{2} - (2k + 1)x + k = 0$ 为一元二次方程,故 $k \neq 0$。
方程有两个不相等的实数根,则判别式 $\Delta > 0$,即:
$\Delta = (2k + 1)^{2} - 4k \cdot k = 4k^{2} + 4k + 1 - 4k^{2} = 4k + 1 > 0$,
解不等式 $4k + 1 > 0$,得 $k > -\frac{1}{4}$。
综合 $k \neq 0$ 和 $k > -\frac{1}{4}$,得 $k$ 的取值范围为 $k > -\frac{1}{4}$ 且 $k \neq 0$。
方程有两个不相等的实数根,则判别式 $\Delta > 0$,即:
$\Delta = (2k + 1)^{2} - 4k \cdot k = 4k^{2} + 4k + 1 - 4k^{2} = 4k + 1 > 0$,
解不等式 $4k + 1 > 0$,得 $k > -\frac{1}{4}$。
综合 $k \neq 0$ 和 $k > -\frac{1}{4}$,得 $k$ 的取值范围为 $k > -\frac{1}{4}$ 且 $k \neq 0$。
12. 如图,一个$Rt\triangle ABC的斜边AB$恰好与量角器的零刻度线的两个端点重合,点$D对应的示数为56^{\circ}$,则$\angle BCD$的度数为______
62°
.zyjl.cn/pic18/2025-09-08/6222c8dd47d06e740f6752008218b23e.jpg?x-oss-process=image/crop,x_594,y_1032,w_246,h_354">答案:62°
解析:
连接OD,O为AB中点(量角器中心),则OA=OB=OD。点D示数56°即圆心角∠AOD=56°,故弧AD=56°。AB为直径,Rt△ABC中∠ACB=90°,C在以AB为直径的圆上,A、B、C、D四点共圆。弧BD=180°-弧AD=124°,∠BCD为弧BD所对圆周角,故∠BCD=1/2弧BD=62°。
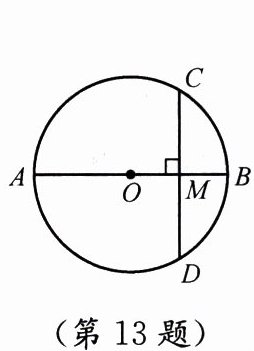
13. 如图,$AB是\odot O$的直径,弦$CD\perp AB$,垂足为$M$,$AB = 26$,$OM = 5$,则$CD$的长为
24
.
答案:$24$
解析:
连接$OC$,由于$AB$是$\odot O$的直径,所以$OA = OB = OC = \frac{AB}{2} = 13$,
已知$OM = 5$,则在$Rt \bigtriangleup OCM$中,利用勾股定理,有$CM = \sqrt{OC^{2} - OM^{2}} = \sqrt{13^{2} - 5^{2}} = 12$,
由于$CD \perp AB$,根据垂径定理,知道$CM = MD$,
所以,$CD = 2CM = 24$。
已知$OM = 5$,则在$Rt \bigtriangleup OCM$中,利用勾股定理,有$CM = \sqrt{OC^{2} - OM^{2}} = \sqrt{13^{2} - 5^{2}} = 12$,
由于$CD \perp AB$,根据垂径定理,知道$CM = MD$,
所以,$CD = 2CM = 24$。
14. 如图,一转盘被分成面积相等的9份,转动转盘,指针指向偶数的概率是

$\frac{4}{9}$
.
答案:$\frac{4}{9}$
解析:
转盘被分成9份,每份面积相等。
数字为1,2,3,4,5,6,7,8,9。
其中偶数有2,4,6,8,共4个。
总共有9个等可能的结果,所以指针指向偶数的概率为$\frac{4}{9}$。
数字为1,2,3,4,5,6,7,8,9。
其中偶数有2,4,6,8,共4个。
总共有9个等可能的结果,所以指针指向偶数的概率为$\frac{4}{9}$。
15. 如图,$PA、PB分别切\odot O于点A、B$,$\angle APB = 50^{\circ}$,则$\angle AOP= $

65
$^{\circ}$.
答案:65
解析:
∵PA、PB分别切⊙O于点A、B,∴OA⊥PA,OP平分∠APB,∠OPA=∠OPB=25°,∴∠OAP=90°,∴∠AOP=90°-25°=65°
16. 有三张正面分别写有数$-1、1、2$的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数作为$a$的值,再从剩余的两张卡片中随机抽取一张,以其正面的数作为$b$的值,则点$(a,b)$在第二象限的概率为
1/3
.答案:1/3
解析:
列表如下:
|第一次抽取|第二次抽取|点(a,b)|象限|
|----|----|----|----|
|-1|1|(-1,1)|第二象限|
|-1|2|(-1,2)|第二象限|
|1|-1|(1,-1)|第四象限|
|1|2|(1,2)|第一象限|
|2|-1|(2,-1)|第四象限|
|2|1|(2,1)|第一象限|
共有6种等可能结果,其中在第二象限的有2种,概率为2/6=1/3。
|第一次抽取|第二次抽取|点(a,b)|象限|
|----|----|----|----|
|-1|1|(-1,1)|第二象限|
|-1|2|(-1,2)|第二象限|
|1|-1|(1,-1)|第四象限|
|1|2|(1,2)|第一象限|
|2|-1|(2,-1)|第四象限|
|2|1|(2,1)|第一象限|
共有6种等可能结果,其中在第二象限的有2种,概率为2/6=1/3。
17. 解下列方程(每题4分,共12分):
(1) $2x^{2}+4x - 1 = 0$;
(2) $x^{2}-7x - 60 = 0$;
(3) $(x - 5)^{2}= 5 - x$.
(1) $2x^{2}+4x - 1 = 0$;
(2) $x^{2}-7x - 60 = 0$;
(3) $(x - 5)^{2}= 5 - x$.
答案:(1)
已知方程$2x^{2}+4x - 1 = 0$,其中$a = 2$,$b = 4$,$c = -1$。
根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,先计算判别式$\Delta=b^{2}-4ac$:
$\Delta = 4^{2}-4×2×(-1)=16 + 8 = 24$
则$x=\frac{-4\pm\sqrt{24}}{2×2}=\frac{-4\pm2\sqrt{6}}{4}=\frac{-2\pm\sqrt{6}}{2}$
所以$x_{1}=\frac{-2 + \sqrt{6}}{2}$,$x_{2}=\frac{-2-\sqrt{6}}{2}$。
(2)
对于方程$x^{2}-7x - 60 = 0$,分解因式得$(x - 12)(x + 5)=0$。
则$x - 12 = 0$或$x + 5 = 0$。
解得$x_{1}=12$,$x_{2}=-5$。
(3)
由$(x - 5)^{2}=5 - x$,移项得$(x - 5)^{2}+(x - 5)=0$。
提取公因式$(x - 5)$得$(x - 5)(x - 5 + 1)=0$,即$(x - 5)(x - 4)=0$。
则$x - 5 = 0$或$x - 4 = 0$。
解得$x_{1}=5$,$x_{2}=4$。
已知方程$2x^{2}+4x - 1 = 0$,其中$a = 2$,$b = 4$,$c = -1$。
根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,先计算判别式$\Delta=b^{2}-4ac$:
$\Delta = 4^{2}-4×2×(-1)=16 + 8 = 24$
则$x=\frac{-4\pm\sqrt{24}}{2×2}=\frac{-4\pm2\sqrt{6}}{4}=\frac{-2\pm\sqrt{6}}{2}$
所以$x_{1}=\frac{-2 + \sqrt{6}}{2}$,$x_{2}=\frac{-2-\sqrt{6}}{2}$。
(2)
对于方程$x^{2}-7x - 60 = 0$,分解因式得$(x - 12)(x + 5)=0$。
则$x - 12 = 0$或$x + 5 = 0$。
解得$x_{1}=12$,$x_{2}=-5$。
(3)
由$(x - 5)^{2}=5 - x$,移项得$(x - 5)^{2}+(x - 5)=0$。
提取公因式$(x - 5)$得$(x - 5)(x - 5 + 1)=0$,即$(x - 5)(x - 4)=0$。
则$x - 5 = 0$或$x - 4 = 0$。
解得$x_{1}=5$,$x_{2}=4$。