18. (8分)现定义运算“★”,对于任意实数$a、b$,都有$a★b = a^{2}-3a + b$,如:$3★5 = 3^{2}-3×3 + 5$.若$x★2 = 6$,则实数$x$的值是多少?
答案:由题意得,$x★2 = x^{2}-3x + 2$。
因为$x★2 = 6$,所以$x^{2}-3x + 2 = 6$。
移项得$x^{2}-3x - 4 = 0$。
因式分解得$(x - 4)(x + 1) = 0$。
则$x - 4 = 0$或$x + 1 = 0$。
解得$x = 4$或$x = -1$。
答:实数$x$的值是$4$或$-1$。
因为$x★2 = 6$,所以$x^{2}-3x + 2 = 6$。
移项得$x^{2}-3x - 4 = 0$。
因式分解得$(x - 4)(x + 1) = 0$。
则$x - 4 = 0$或$x + 1 = 0$。
解得$x = 4$或$x = -1$。
答:实数$x$的值是$4$或$-1$。
19. (8分)当$x满足条件\begin{cases}x + 1\lt3x - 3,\frac{1}{2}(x - 4)\lt\frac{1}{3}(x - 4)\end{cases} $时,求方程$x^{2}-2x - 4 = 0$的根.
答案:首先解不等式组:
$\begin{cases}x + 1 \lt 3x - 3, \quad (①) \\ \frac{1}{2}(x - 4) \lt \frac{1}{3}(x - 4)\quad (②)\end{cases}$
解不等式$①$:
$x + 1 \lt 3x - 3$
$2x \gt 4$
$x \gt 2$
解不等式$②$:
$\frac{1}{2}(x - 4) \lt \frac{1}{3}(x - 4)$
$3(x - 4) \lt 2(x - 4)$
$3x - 12 \lt 2x - 8$
$x \lt 4$
综合不等式$①$和$②$的解集,得到不等式组的解集为:
$2 \lt x \lt 4$
接下来解方程$x^{2} - 2x - 4 = 0$:
使用求根公式:
$x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$
其中,$a = 1, b = -2, c = -4$。
代入得:
$x = \frac{2 \pm \sqrt{(-2)^{2} - 4 × 1 × (-4)}}{2 × 1}$
$x = \frac{2 \pm \sqrt{20}}{2}$
$x = 1 \pm \sqrt{5},$
由于$2 \lt 1 + \sqrt{5} \lt 4$,且$1 - \sqrt{5} \lt 2$(不满足条件,舍去),
所以方程在给定条件下的根为:
$x = 1 + \sqrt{5}$,
综上所述,本题答案是:$x = 1 + \sqrt{5}$。
$\begin{cases}x + 1 \lt 3x - 3, \quad (①) \\ \frac{1}{2}(x - 4) \lt \frac{1}{3}(x - 4)\quad (②)\end{cases}$
解不等式$①$:
$x + 1 \lt 3x - 3$
$2x \gt 4$
$x \gt 2$
解不等式$②$:
$\frac{1}{2}(x - 4) \lt \frac{1}{3}(x - 4)$
$3(x - 4) \lt 2(x - 4)$
$3x - 12 \lt 2x - 8$
$x \lt 4$
综合不等式$①$和$②$的解集,得到不等式组的解集为:
$2 \lt x \lt 4$
接下来解方程$x^{2} - 2x - 4 = 0$:
使用求根公式:
$x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$
其中,$a = 1, b = -2, c = -4$。
代入得:
$x = \frac{2 \pm \sqrt{(-2)^{2} - 4 × 1 × (-4)}}{2 × 1}$
$x = \frac{2 \pm \sqrt{20}}{2}$
$x = 1 \pm \sqrt{5},$
由于$2 \lt 1 + \sqrt{5} \lt 4$,且$1 - \sqrt{5} \lt 2$(不满足条件,舍去),
所以方程在给定条件下的根为:
$x = 1 + \sqrt{5}$,
综上所述,本题答案是:$x = 1 + \sqrt{5}$。
20. (10分)某校对九年级各个班级教室的卫生情况的考核包括以下几项:黑板、门窗、桌椅、地面,某日3个班级的各项卫生成绩分别如下表:
| 项目 | 九年级(1)班 | 九年级(2)班 | 九年级(3)班 |
| 黑板 | $90$ | $90$ | $85$ |
| 门窗 | $90$ | $95$ | $90$ |
| 桌椅 | $90$ | $85$ | $90$ |
| 地面 | $85$ | $90$ | $95$ |
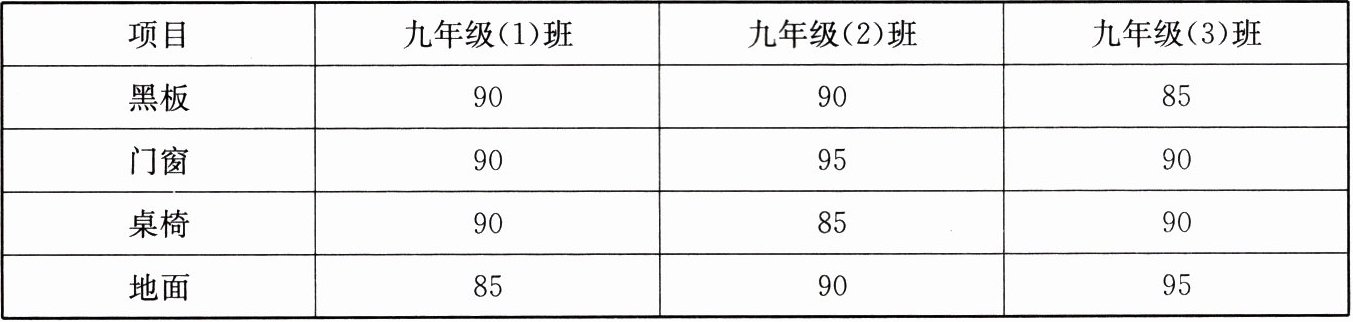
(1) 求每个班的平均分;
(2) 如果将黑板、门窗、桌椅、地面这4项得分依次按15%、10%、35%、40%的比例计算卫生总成绩,那么哪个班的成绩最高?
| 项目 | 九年级(1)班 | 九年级(2)班 | 九年级(3)班 |
| 黑板 | $90$ | $90$ | $85$ |
| 门窗 | $90$ | $95$ | $90$ |
| 桌椅 | $90$ | $85$ | $90$ |
| 地面 | $85$ | $90$ | $95$ |

(1) 求每个班的平均分;
(2) 如果将黑板、门窗、桌椅、地面这4项得分依次按15%、10%、35%、40%的比例计算卫生总成绩,那么哪个班的成绩最高?
答案:(1)九年级(1)班平均分:$(90 + 90 + 90 + 85)÷4 = 88.75$
九年级(2)班平均分:$(90 + 95 + 85 + 90)÷4 = 90$
九年级(3)班平均分:$(85 + 90 + 90 + 95)÷4 = 90$
(2)九年级(1)班总成绩:$90×15\% + 90×10\% + 90×35\% + 85×40\% = 88$
九年级(2)班总成绩:$90×15\% + 95×10\% + 85×35\% + 90×40\% = 89.25$
九年级(3)班总成绩:$85×15\% + 90×10\% + 90×35\% + 95×40\% = 91.25$
$91.25 > 89.25 > 88$,九年级(3)班成绩最高
(1)三个班平均分分别为88.75、90、90;(2)九年级(3)班成绩最高。
九年级(2)班平均分:$(90 + 95 + 85 + 90)÷4 = 90$
九年级(3)班平均分:$(85 + 90 + 90 + 95)÷4 = 90$
(2)九年级(1)班总成绩:$90×15\% + 90×10\% + 90×35\% + 85×40\% = 88$
九年级(2)班总成绩:$90×15\% + 95×10\% + 85×35\% + 90×40\% = 89.25$
九年级(3)班总成绩:$85×15\% + 90×10\% + 90×35\% + 95×40\% = 91.25$
$91.25 > 89.25 > 88$,九年级(3)班成绩最高
(1)三个班平均分分别为88.75、90、90;(2)九年级(3)班成绩最高。