2. ⊙O的直径为6cm,当OP= 3cm时,点P在
⊙O上
;当OP≤3cm
时,点P不在⊙O外.答案:⊙O上;≤3cm
解析:
⊙O的直径为6cm,则半径r=3cm。当OP=3cm时,OP=r,所以点P在⊙O上;当点P不在⊙O外时,OP≤r,即OP≤3cm。
3. 已知⊙O的圆心与坐标原点重合,半径为r.若点A(2,0)在⊙O内,点P(2,2)在⊙O外,则r的取值范围是
$2 < r< 2\sqrt{2}$
.答案:$2 < r< 2\sqrt{2}$(写实际范围,不写选项)。
解析:
由于点$A(2,0)$在圆内,根据圆内点的性质,有:
$OA < r$,
即:
$\sqrt{2^2 + 0^2} < r$,
$2 < r$,
同样,由于点$P(2,2)$在圆外,根据圆外点的性质,有:
$OP > r$,
即:
$\sqrt{2^2 + 2^2} > r$,
$2\sqrt{2} > r$,
综合以上两个不等式,得到r的取值范围为:
$2 < r < 2\sqrt{2}$,
$OA < r$,
即:
$\sqrt{2^2 + 0^2} < r$,
$2 < r$,
同样,由于点$P(2,2)$在圆外,根据圆外点的性质,有:
$OP > r$,
即:
$\sqrt{2^2 + 2^2} > r$,
$2\sqrt{2} > r$,
综合以上两个不等式,得到r的取值范围为:
$2 < r < 2\sqrt{2}$,
4. 在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.下列说法中,不正确的是(
A.当a<5时,点B在⊙A内
B.当1<a<5时,点B在⊙A内
C.当a<1时,点B在⊙A外
D.当a>5时,点B在⊙A外
A
)A.当a<5时,点B在⊙A内
B.当1<a<5时,点B在⊙A内
C.当a<1时,点B在⊙A外
D.当a>5时,点B在⊙A外
答案:A
解析:
点A表示的实数为3,⊙A半径为2,则⊙A在数轴上对应的区间为(3 - 2, 3 + 2) = (1, 5)。
选项A:当a < 5时,a可能在1到5之间(内),也可能小于1(外),故说法不正确。
选项B:1 < a < 5时,点B在⊙A内,正确。
选项C:a < 1时,点B在⊙A外,正确。
选项D:a > 5时,点B在⊙A外,正确。
选项A:当a < 5时,a可能在1到5之间(内),也可能小于1(外),故说法不正确。
选项B:1 < a < 5时,点B在⊙A内,正确。
选项C:a < 1时,点B在⊙A外,正确。
选项D:a > 5时,点B在⊙A外,正确。
5. 设MN= 2cm.画图说明具有下列性质的点的集合是怎样的图形.
(1) 到点M的距离等于1.5cm的点的集合;
(2) 到点N的距离等于1.5cm的点的集合;
(3) 到点M的距离小于1.5cm,而到点N的距离大于1.5cm的点的集合(用阴影表示);
(4) 在所画的图形中,你还能再提出一个关于点的集合的问题吗?
(1) 到点M的距离等于1.5cm的点的集合;
(2) 到点N的距离等于1.5cm的点的集合;
(3) 到点M的距离小于1.5cm,而到点N的距离大于1.5cm的点的集合(用阴影表示);
(4) 在所画的图形中,你还能再提出一个关于点的集合的问题吗?
答案:(1)到点$M$的距离等于$1.5cm$的点的集合:
以点$M$为圆心,$1.5cm$为半径画圆,该圆即为所求的点的集合。
(2)到点$N$的距离等于$1.5cm$的点的集合:
以点$N$为圆心,$1.5cm$为半径画圆,该圆即为所求的点的集合。
(3) 分别以M,N为圆心,以$1.5cm$,$1.5cm$为半径画圆(圆M与圆N)。
在圆N内部(不包括圆N本身)且在圆M外部(不包括圆M本身)的区域打上阴影,该阴影区域即为所求的点的集合。
(4)问题:到点$M$和点$N$的距离都等于或小于$1cm$的点的集合是怎样的图形(答案不唯一)。
以点$M$为圆心,$1.5cm$为半径画圆,该圆即为所求的点的集合。
(2)到点$N$的距离等于$1.5cm$的点的集合:
以点$N$为圆心,$1.5cm$为半径画圆,该圆即为所求的点的集合。
(3) 分别以M,N为圆心,以$1.5cm$,$1.5cm$为半径画圆(圆M与圆N)。
在圆N内部(不包括圆N本身)且在圆M外部(不包括圆M本身)的区域打上阴影,该阴影区域即为所求的点的集合。
(4)问题:到点$M$和点$N$的距离都等于或小于$1cm$的点的集合是怎样的图形(答案不唯一)。
1. 已知AB为⊙O的直径,P为⊙O上任意一点(不与点A、B重合),则点P关于AB的对称点P′与⊙O的位置关系为(
A.在⊙O内
B.在⊙O外
C.在⊙O上
D.不能确定
C
)A.在⊙O内
B.在⊙O外
C.在⊙O上
D.不能确定
答案:C
解析:
设圆心为$O$,$AB$是直径,点$P$在圆上,则$OP$等于半径$r$。
点$P'$是点$P$关于直线$AB$的对称点,所以$OP' = OP = r$。
由于$OP'$等于圆的半径,因此点$P'$也在圆上。
点$P'$是点$P$关于直线$AB$的对称点,所以$OP' = OP = r$。
由于$OP'$等于圆的半径,因此点$P'$也在圆上。
2. 木杆AB斜靠在墙壁上,当木杆的顶端A沿墙壁NO竖直下滑时,木杆的底端B也随之沿地面OM水平向右滑动.下图中虚线表示木杆的中点P变化的轨迹,其中正确的是(
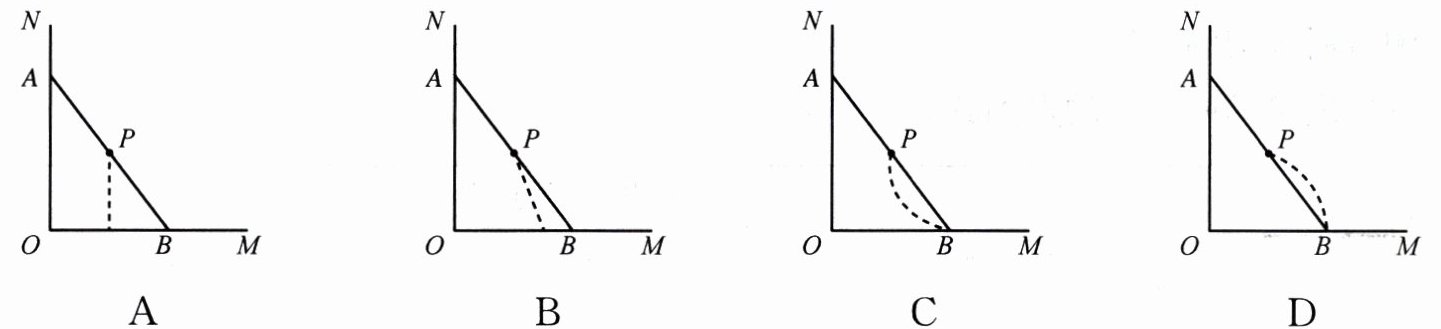
D
)
答案:D
解析:
连接OP,因NO⊥OM,故△AOB为直角三角形。P为AB中点,由直角三角形斜边上的中线性质知OP=1/2AB。木杆AB长度不变,故OP为定值。根据圆的定义,P点轨迹是以O为圆心、OP为半径的圆的一部分(第一象限内的四分之一圆弧)。观察选项,D符合圆弧轨迹。
3. 在矩形ABCD中,AB= 6,AD= 8.若作⊙A,使B,C,D三点至少有一点在⊙A内,至少有一点在⊙A外,则⊙A的半径r的取值范围是
6< r < 10
.答案:$6< r < 10$(以题目要求的形式填写答案则为具体数值范围,不以选择形式呈现)。
解析:
在矩形$ABCD$中,已知$AB = 6$,$AD = 8$。
根据矩形的性质$AC$(对角线)的长度可通过勾股定理计算,
即$AC = \sqrt{AB^{2} + AD^{2}} = \sqrt{6^{2} + 8^{2}} = 10$。
分析三点$B$,$C$,$D$到圆心$A$的距离:
$B$点到$A$点的距离为$AB = 6$。
$D$点到$A$点的距离为$AD = 8$。
$C$点到$A$点的距离为$AC = 10$。
根据题意,要求至少有一点在圆内,至少有一点在圆外,可以得到以下不等式:
$6< r < 10$(因为$AB$是最小的距离,保证$B$在圆内,而$AC$是最大的距离,保证$C$在圆外)。
根据矩形的性质$AC$(对角线)的长度可通过勾股定理计算,
即$AC = \sqrt{AB^{2} + AD^{2}} = \sqrt{6^{2} + 8^{2}} = 10$。
分析三点$B$,$C$,$D$到圆心$A$的距离:
$B$点到$A$点的距离为$AB = 6$。
$D$点到$A$点的距离为$AD = 8$。
$C$点到$A$点的距离为$AC = 10$。
根据题意,要求至少有一点在圆内,至少有一点在圆外,可以得到以下不等式:
$6< r < 10$(因为$AB$是最小的距离,保证$B$在圆内,而$AC$是最大的距离,保证$C$在圆外)。
4. 如图,在某海域中,以点A为圆心、3km为半径的圆形区域为暗礁区.救援船要从点B处前往点A处,A、B两点之间的距离是10km,如果救援船始终保持10km/h的速度行驶,那么在什么时段内,救援船是安全的? 救援船何时进入暗礁区域?


答案:1. 首先计算救援船从$B$到$C$的时间:
已知$AB = 10km$,$AC = 3km$,则$BC=AB - AC$。
根据公式$t=\frac{s}{v}$(其中$t$为时间,$s$为路程,$v$为速度),$v = 10km/h$。
$BC$的距离$s_{BC}=10 - 3=7km$。
那么救援船从$B$到$C$的时间$t_{1}=\frac{s_{BC}}{v}=\frac{7}{10}=0.7h$。
救援船从$B$到$A$的时间$t_{2}=\frac{AB}{v}=\frac{10}{10}=1h$。
2. 然后分析安全时段和进入暗礁时间:
救援船在$0$到$0.7h$这个时段内是安全的(因为在$0$到$0.7h$时,救援船还未到达暗礁区边界$C$点)。
救援船在$0.7h$时进入暗礁区域(当行驶时间为$t = 0.7h$时,刚好到达暗礁区边界$C$点)。
答:在$0$到$0.7h$时段内救援船是安全的,救援船在$0.7h$时进入暗礁区域。
已知$AB = 10km$,$AC = 3km$,则$BC=AB - AC$。
根据公式$t=\frac{s}{v}$(其中$t$为时间,$s$为路程,$v$为速度),$v = 10km/h$。
$BC$的距离$s_{BC}=10 - 3=7km$。
那么救援船从$B$到$C$的时间$t_{1}=\frac{s_{BC}}{v}=\frac{7}{10}=0.7h$。
救援船从$B$到$A$的时间$t_{2}=\frac{AB}{v}=\frac{10}{10}=1h$。
2. 然后分析安全时段和进入暗礁时间:
救援船在$0$到$0.7h$这个时段内是安全的(因为在$0$到$0.7h$时,救援船还未到达暗礁区边界$C$点)。
救援船在$0.7h$时进入暗礁区域(当行驶时间为$t = 0.7h$时,刚好到达暗礁区边界$C$点)。
答:在$0$到$0.7h$时段内救援船是安全的,救援船在$0.7h$时进入暗礁区域。