1. 已知圆锥的底面半径是 $ 2 $ cm,母线长是 $ 5 $ cm,它的侧面积是
$10\pi$
$ cm^2 $。答案:$10\pi$
解析:
圆锥的侧面积公式为 $S = \pi r l$,其中 $r$ 是底面半径,$l$ 是母线长。
根据题目,底面半径 $r = 2$ cm,母线长 $l = 5$ cm。
代入公式得:
$S = \pi × 2 × 5 = 10\pi$($cm^2$)
根据题目,底面半径 $r = 2$ cm,母线长 $l = 5$ cm。
代入公式得:
$S = \pi × 2 × 5 = 10\pi$($cm^2$)
2. 已知圆锥的母线长是 $ 10 $ cm,侧面积是 $ 60\pi $ $ cm^2 $,它的底面半径是
6
cm。答案:6
解析:
设圆锥底面半径为$r$cm,母线长$l = 10$cm。圆锥侧面积公式为$S = \pi rl$,已知侧面积$S = 60\pi$,则$\pi r × 10 = 60\pi$,解得$r = 6$。
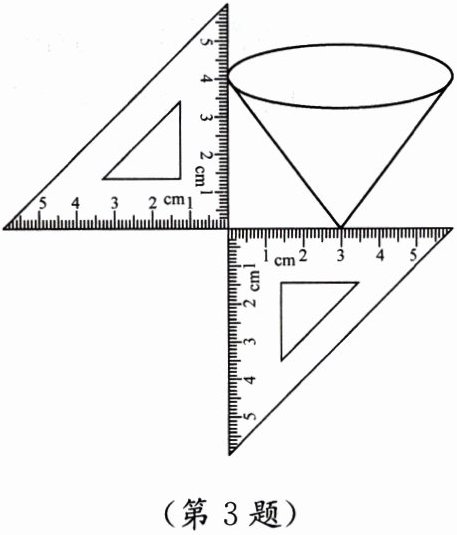
3. 如图,某同学用三角板测量一个圆锥形漏斗的高度,该圆锥形漏斗的侧面积为
$ 15\pi $
$ cm^2 $。
答案:$ 15\pi $
解析:
由图可知,圆锥底面半径$ r = 3\space cm $,高$ h = 4\space cm $。母线$ l = \sqrt{r^{2}+h^{2}}=\sqrt{3^{2}+4^{2}} = 5\space cm $。侧面积$ S=\pi rl=\pi×3×5 = 15\pi\space cm^{2} $。
4. 若圆锥的侧面积恰好等于其底面积的 $ 2 $ 倍,则圆锥侧面展开图所对应的扇形圆心角的度数为(
A.$ 60^{\circ} $
B.$ 90^{\circ} $
C.$ 120^{\circ} $
D.$ 180^{\circ} $
D
)A.$ 60^{\circ} $
B.$ 90^{\circ} $
C.$ 120^{\circ} $
D.$ 180^{\circ} $
答案:D
解析:
设圆锥的底面半径为 $r$,母线长为 $l$,圆锥侧面展开图所对应的扇形圆心角为 $n{^\circ}$。
圆锥的底面积为$\pi r^{2}$,圆锥的侧面积为$\pi rl$(其中$r$为底面半径,$l$为母线长)。
根据题意,圆锥的侧面积恰好等于其底面积的$2$倍,即:
$\pi rl = 2\pi r^{2}$,
由于$r \neq 0$(圆锥的底面半径不可能为$0$),可以两边同时除以$\pi r$,得到:
$l = 2r$,
圆锥侧面展开图是一个扇形,其弧长等于圆锥底面的周长,即:
$2\pi r = \frac{n\pi l}{180}$,
将$l = 2r$代入上式,得到:
$2\pi r = \frac{n\pi \cdot 2r}{180}$,
同样由于$r \neq 0$,可以两边同时除以$2\pi r$并乘以$180$,得到:
$n = 180$。
圆锥的底面积为$\pi r^{2}$,圆锥的侧面积为$\pi rl$(其中$r$为底面半径,$l$为母线长)。
根据题意,圆锥的侧面积恰好等于其底面积的$2$倍,即:
$\pi rl = 2\pi r^{2}$,
由于$r \neq 0$(圆锥的底面半径不可能为$0$),可以两边同时除以$\pi r$,得到:
$l = 2r$,
圆锥侧面展开图是一个扇形,其弧长等于圆锥底面的周长,即:
$2\pi r = \frac{n\pi l}{180}$,
将$l = 2r$代入上式,得到:
$2\pi r = \frac{n\pi \cdot 2r}{180}$,
同样由于$r \neq 0$,可以两边同时除以$2\pi r$并乘以$180$,得到:
$n = 180$。