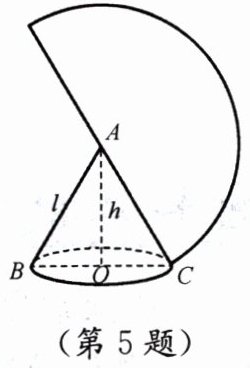
5. 如图,一个圆锥的高为 $ 3\sqrt{3} $,其侧面展开图是半圆。
(1)求圆锥母线长与底面半径的比值;
(2)求该圆锥的全面积。
(1)求圆锥母线长与底面半径的比值;
(2)求该圆锥的全面积。

答案:(1)设圆锥母线长为$l$,底面半径为$r$。
∵侧面展开图是半圆,∴侧面展开图弧长为$\pi l$。
又∵圆锥底面周长为$2\pi r$,且侧面展开图弧长等于底面周长,
∴$\pi l = 2\pi r$,即$l = 2r$。
∴母线长与底面半径的比值为$2$。
(2)∵圆锥高$h = 3\sqrt{3}$,由勾股定理得$l^2 = r^2 + h^2$。
又$l = 2r$,∴$(2r)^2 = r^2 + (3\sqrt{3})^2$,
即$4r^2 = r^2 + 27$,解得$r^2 = 9$,$r = 3$($r>0$),则$l = 6$。
侧面积$S_{侧} = \frac{1}{2}\pi l^2 = \frac{1}{2}\pi×6^2 = 18\pi$,
底面积$S_{底} = \pi r^2 = 9\pi$,
全面积$S_{全} = S_{侧} + S_{底} = 18\pi + 9\pi = 27\pi$。
(1) $2$;(2) $27\pi$
∵侧面展开图是半圆,∴侧面展开图弧长为$\pi l$。
又∵圆锥底面周长为$2\pi r$,且侧面展开图弧长等于底面周长,
∴$\pi l = 2\pi r$,即$l = 2r$。
∴母线长与底面半径的比值为$2$。
(2)∵圆锥高$h = 3\sqrt{3}$,由勾股定理得$l^2 = r^2 + h^2$。
又$l = 2r$,∴$(2r)^2 = r^2 + (3\sqrt{3})^2$,
即$4r^2 = r^2 + 27$,解得$r^2 = 9$,$r = 3$($r>0$),则$l = 6$。
侧面积$S_{侧} = \frac{1}{2}\pi l^2 = \frac{1}{2}\pi×6^2 = 18\pi$,
底面积$S_{底} = \pi r^2 = 9\pi$,
全面积$S_{全} = S_{侧} + S_{底} = 18\pi + 9\pi = 27\pi$。
(1) $2$;(2) $27\pi$
1. 用一块圆心角为 $ 120^{\circ} $ 的扇形铁皮围成一个底面直径为 $ 10 $ cm 的圆锥形工件的侧面,这个圆锥的高是
$10\sqrt{2}$
cm。答案:$10\sqrt{2}$
解析:
本题可先根据圆锥底面直径求出底面周长,再结合扇形弧长公式求出扇形半径,最后根据圆锥的母线长、底面半径与高构成直角三角形,利用勾股定理求出圆锥的高。
步骤一:求圆锥底面周长$C$。
已知圆锥底面直径为$10cm$,根据圆的周长公式$C = \pi d$(其中$d$为圆的直径),可得圆锥底面周长$C = 10\pi cm$。
步骤二:求扇形半径$R$(即圆锥母线长)。
因为该扇形铁皮围成圆锥形工件的侧面,所以扇形的弧长等于圆锥底面周长,即$l = 10\pi cm$。
已知扇形圆心角$n = 120^{\circ}$,根据扇形弧长公式$l=\frac{n\pi R}{180}$(其中$R$为扇形半径),可得$10\pi=\frac{120\pi R}{180}$,
等式两边同时除以$\pi$得$10=\frac{120R}{180}$,
等式两边同时乘以$180$得$120R = 10×180$,
即$120R = 1800$,
解得$R = 15cm$,所以圆锥母线长为$15cm$。
步骤三:求圆锥的高$h$。
已知圆锥底面直径为$10cm$,则底面半径$r = 5cm$,圆锥的母线长$R = 15cm$。
由于圆锥的母线长、底面半径与高构成直角三角形,其中母线为斜边,根据勾股定理$h = \sqrt{R^{2}-r^{2}}$,可得:
$h = \sqrt{15^{2}-5^{2}}=\sqrt{225 - 25}=\sqrt{200}=10\sqrt{2}cm$。
步骤一:求圆锥底面周长$C$。
已知圆锥底面直径为$10cm$,根据圆的周长公式$C = \pi d$(其中$d$为圆的直径),可得圆锥底面周长$C = 10\pi cm$。
步骤二:求扇形半径$R$(即圆锥母线长)。
因为该扇形铁皮围成圆锥形工件的侧面,所以扇形的弧长等于圆锥底面周长,即$l = 10\pi cm$。
已知扇形圆心角$n = 120^{\circ}$,根据扇形弧长公式$l=\frac{n\pi R}{180}$(其中$R$为扇形半径),可得$10\pi=\frac{120\pi R}{180}$,
等式两边同时除以$\pi$得$10=\frac{120R}{180}$,
等式两边同时乘以$180$得$120R = 10×180$,
即$120R = 1800$,
解得$R = 15cm$,所以圆锥母线长为$15cm$。
步骤三:求圆锥的高$h$。
已知圆锥底面直径为$10cm$,则底面半径$r = 5cm$,圆锥的母线长$R = 15cm$。
由于圆锥的母线长、底面半径与高构成直角三角形,其中母线为斜边,根据勾股定理$h = \sqrt{R^{2}-r^{2}}$,可得:
$h = \sqrt{15^{2}-5^{2}}=\sqrt{225 - 25}=\sqrt{200}=10\sqrt{2}cm$。
2. 如图,有一直径是 $ \sqrt{2} $ m 的圆形铁皮,现从中剪出一个圆周角是 $ 90^{\circ} $ 的最大扇形 $ ABC $。
(1) $ AB $ 的长为
(2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆半径。
(1) $ AB $ 的长为
1
m;(2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆半径。
所得圆锥的底面圆半径为$\frac{1}{4}\ m$。
答案:(1)1;(2)1/4 m
解析:
(1)圆形铁皮直径为√2 m,半径为√2/2 m。扇形ABC中∠BAC=90°,要使扇形最大,A、B、C在圆上,∠BAC=90°,则BC为圆的直径(90°圆周角所对弦为直径),故BC=√2 m。在Rt△ABC中,AB=AC,由勾股定理AB²+AC²=BC²,即2AB²=(√2)²=2,解得AB=1 m。
(2)扇形半径AB=1 m,圆心角90°,弧长l=90·π·1/180=π/2 m。圆锥底面圆周长=弧长,即2πr=π/2,解得r=1/4 m。
(2)扇形半径AB=1 m,圆心角90°,弧长l=90·π·1/180=π/2 m。圆锥底面圆周长=弧长,即2πr=π/2,解得r=1/4 m。
3. 在 $ Rt\triangle ABC $ 中, $ \angle ACB = 90^{\circ} $, $ BC = 4 $, $ AC = 3 $,若将 $ \triangle ABC $ 绕边 $ AB $ 所在直线旋转一周,求所得几何体的表面积。
答案:在Rt△ABC中,∠ACB=90°,BC=4,AC=3。
1. 求斜边AB:由勾股定理,AB²=AC²+BC²=3²+4²=25,得AB=5。
2. 求斜边上的高CD:由面积公式,1/2×AC×BC=1/2×AB×CD,即1/2×3×4=1/2×5×CD,解得CD=12/5(即底面半径r=12/5)。
3. 旋转后几何体为两个同底圆锥的组合体,母线长分别为AC=3和BC=4。
4. 圆锥侧面积公式S=πrl,两圆锥侧面积之和为表面积:
S=π×r×AC + π×r×BC=π×(12/5)×3 + π×(12/5)×4=36π/5 + 48π/5=84π/5。
所得几何体的表面积为84π/5。
1. 求斜边AB:由勾股定理,AB²=AC²+BC²=3²+4²=25,得AB=5。
2. 求斜边上的高CD:由面积公式,1/2×AC×BC=1/2×AB×CD,即1/2×3×4=1/2×5×CD,解得CD=12/5(即底面半径r=12/5)。
3. 旋转后几何体为两个同底圆锥的组合体,母线长分别为AC=3和BC=4。
4. 圆锥侧面积公式S=πrl,两圆锥侧面积之和为表面积:
S=π×r×AC + π×r×BC=π×(12/5)×3 + π×(12/5)×4=36π/5 + 48π/5=84π/5。
所得几何体的表面积为84π/5。
4. 如图,一圆锥形容器盖的底面半径为 $ 1 $,母线长为 $ 6 $。一只蚂蚁要从底面圆周上一点 $ B $ 出发,沿容器盖侧面爬行一圈再回到点 $ B $,求它爬行的最短路线的长度。


答案:答题
圆锥的底面半径 $ r = 1 $,母线长 $ l = 6 $。
圆锥底面周长:
$C = 2\pi r = 2\pi × 1 = 2\pi$。
设圆锥侧面展开图的扇形角度为 $ \theta $,则:
$l × \theta = C \implies 6 × \theta = 2\pi \implies \theta = \frac{\pi}{3}$。
在展开的扇形中,蚂蚁爬行的最短路线即为扇形的弦长。
弦长公式为:
$L = 2l \sin\left(\frac{\theta}{2}\right) = 2 × 6 × \sin\left(\frac{\pi}{6}\right) = 12 × \frac{1}{2} = 6$。
它爬行的最短路线的长度为$6$。
圆锥的底面半径 $ r = 1 $,母线长 $ l = 6 $。
圆锥底面周长:
$C = 2\pi r = 2\pi × 1 = 2\pi$。
设圆锥侧面展开图的扇形角度为 $ \theta $,则:
$l × \theta = C \implies 6 × \theta = 2\pi \implies \theta = \frac{\pi}{3}$。
在展开的扇形中,蚂蚁爬行的最短路线即为扇形的弦长。
弦长公式为:
$L = 2l \sin\left(\frac{\theta}{2}\right) = 2 × 6 × \sin\left(\frac{\pi}{6}\right) = 12 × \frac{1}{2} = 6$。
它爬行的最短路线的长度为$6$。