1. 下列各式从左到右的变形,是因式分解的是(
A.$3x^{2}+2x = x(3x + 2)$
B.$x^{2}-x - 2 = x(x - 1)-2$
C.$(a + b)(a - b)= a^{2}-b^{2}$
D.$a^{2}b = ab\cdot a$
A
)A.$3x^{2}+2x = x(3x + 2)$
B.$x^{2}-x - 2 = x(x - 1)-2$
C.$(a + b)(a - b)= a^{2}-b^{2}$
D.$a^{2}b = ab\cdot a$
答案:A.
2. 多项式 $9a^{2}x^{2}-18a^{4}x^{3}$,各项的公因式是(
A.$9ax$
B.$9a^{2}x^{2}$
C.$a^{2}x^{2}$
D.$a^{3}x^{2}$
B
)A.$9ax$
B.$9a^{2}x^{2}$
C.$a^{2}x^{2}$
D.$a^{3}x^{2}$
答案:B.
解析:
多项式各项系数的最大公约数是9,相同字母$a$的最低次幂是$a^{2}$,相同字母$x$的最低次幂是$x^{2}$,所以公因式是$9a^{2}x^{2}$。
B.
B.
3. 把多项式 $m^{2}(a - 2)+m(2 - a)$因式分解,结果正确的是(
A.$(a - 2)(m^{2}-m)$
B.$m(a - 2)(m + 1)$
C.$m(a - 2)(m - 1)$
D.$m(2 - a)(m - 1)$
C
)A.$(a - 2)(m^{2}-m)$
B.$m(a - 2)(m + 1)$
C.$m(a - 2)(m - 1)$
D.$m(2 - a)(m - 1)$
答案:C.
解析:
$m^{2}(a - 2)+m(2 - a)$
$=m^{2}(a - 2)-m(a - 2)$
$=m(a - 2)(m - 1)$
C.
$=m^{2}(a - 2)-m(a - 2)$
$=m(a - 2)(m - 1)$
C.
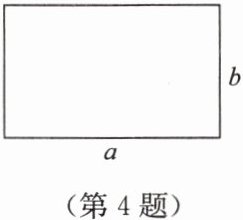
4. 如图,长为 $a$、宽为 $b$ 的长方形的周长为 10,面积为 6,则 $a^{3}b + ab^{3}$ 的值为(
A.15
B.30
C.60
D.78
D
)
A.15
B.30
C.60
D.78
答案:D.
解析:
由题意得,长方形周长为 $2(a + b) = 10$,则 $a + b = 5$;面积为 $ab = 6$。
$a^3b + ab^3 = ab(a^2 + b^2)$,
又 $a^2 + b^2 = (a + b)^2 - 2ab = 5^2 - 2×6 = 25 - 12 = 13$,
所以 $a^3b + ab^3 = 6×13 = 78$。
D.
$a^3b + ab^3 = ab(a^2 + b^2)$,
又 $a^2 + b^2 = (a + b)^2 - 2ab = 5^2 - 2×6 = 25 - 12 = 13$,
所以 $a^3b + ab^3 = 6×13 = 78$。
D.
5. 下列多项式中能用平方差公式分解因式的是(
A.$x^{2}+y^{2}$
B.$x^{3}-y^{2}$
C.$-x^{2}+y^{2}$
D.$-x^{2}-y^{2}$
C
)A.$x^{2}+y^{2}$
B.$x^{3}-y^{2}$
C.$-x^{2}+y^{2}$
D.$-x^{2}-y^{2}$
答案:C.
解析:
平方差公式为$a^{2}-b^{2}=(a+b)(a-b)$,需满足两项式且两项符号相反、均为平方形式。
A选项$x^{2}+y^{2}$两项符号相同,不符合;
B选项$x^{3}-y^{2}$中$x^{3}$不是平方项,不符合;
C选项$-x^{2}+y^{2}=y^{2}-x^{2}$,是两项式,符号相反且均为平方项,符合;
D选项$-x^{2}-y^{2}=-(x^{2}+y^{2})$两项符号相同,不符合。
C
A选项$x^{2}+y^{2}$两项符号相同,不符合;
B选项$x^{3}-y^{2}$中$x^{3}$不是平方项,不符合;
C选项$-x^{2}+y^{2}=y^{2}-x^{2}$,是两项式,符号相反且均为平方项,符合;
D选项$-x^{2}-y^{2}=-(x^{2}+y^{2})$两项符号相同,不符合。
C
6. 下列各式中能用完全平方公式进行因式分解的是(
A.$x^{2}+x + 1$
B.$x^{2}+2x - 1$
C.$x^{2}-1$
D.$x^{2}-6x + 9$
D
)A.$x^{2}+x + 1$
B.$x^{2}+2x - 1$
C.$x^{2}-1$
D.$x^{2}-6x + 9$
答案:D.
解析:
完全平方公式为$(a\pm b)^2=a^2\pm 2ab + b^2$。
选项A:$x^2 + x + 1$,中间项$x$不是$2× x×1$,不符合完全平方公式。
选项B:$x^2 + 2x - 1$,常数项为$-1$,不符合完全平方公式中常数项为正的要求。
选项C:$x^2 - 1$,是平方差形式,不符合完全平方公式。
选项D:$x^2 - 6x + 9 = x^2 - 2× x×3 + 3^2=(x - 3)^2$,符合完全平方公式。
D
选项A:$x^2 + x + 1$,中间项$x$不是$2× x×1$,不符合完全平方公式。
选项B:$x^2 + 2x - 1$,常数项为$-1$,不符合完全平方公式中常数项为正的要求。
选项C:$x^2 - 1$,是平方差形式,不符合完全平方公式。
选项D:$x^2 - 6x + 9 = x^2 - 2× x×3 + 3^2=(x - 3)^2$,符合完全平方公式。
D
7. 若 $x^{2}+(m - 3)x + 4$ 是完全平方式,则 $m$ 的值是(
A.7
B.$-1$
C.$\pm7$
D.7 或 $-1$
D
)A.7
B.$-1$
C.$\pm7$
D.7 或 $-1$
答案:D.
解析:
因为$x^{2}+(m - 3)x + 4$是完全平方式,所以$x^{2}+(m - 3)x + 4=(x\pm2)^{2}$。
当$x^{2}+(m - 3)x + 4=(x + 2)^{2}$时,$(x + 2)^{2}=x^{2}+4x + 4$,则$m - 3=4$,解得$m=7$。
当$x^{2}+(m - 3)x + 4=(x - 2)^{2}$时,$(x - 2)^{2}=x^{2}-4x + 4$,则$m - 3=-4$,解得$m=-1$。
综上,$m$的值是7或$-1$。
D.
当$x^{2}+(m - 3)x + 4=(x + 2)^{2}$时,$(x + 2)^{2}=x^{2}+4x + 4$,则$m - 3=4$,解得$m=7$。
当$x^{2}+(m - 3)x + 4=(x - 2)^{2}$时,$(x - 2)^{2}=x^{2}-4x + 4$,则$m - 3=-4$,解得$m=-1$。
综上,$m$的值是7或$-1$。
D.
8. 已知 $x - y = -4$,则多项式 $\frac{1}{2}x^{2}-xy+\frac{1}{2}y^{2}$ 的值为(
A.4
B.6
C.8
D.10
C
)A.4
B.6
C.8
D.10
答案:C.
解析:
$\begin{aligned}\frac{1}{2}x^{2}-xy+\frac{1}{2}y^{2}&=\frac{1}{2}(x^{2}-2xy+y^{2})\\&=\frac{1}{2}(x - y)^{2}\\\because x - y&=-4\\\therefore 原式&=\frac{1}{2}×(-4)^{2}\\&=\frac{1}{2}×16\\&=8\end{aligned}$
C
C
9. 下列各式中,不能用完全平方公式分解因式的有(
① $x^{2}-10x + 25$;② $4a^{2}+4a - 1$;
③ $x^{2}-2x - 1$;④ $-m^{2}+m-\frac{1}{4}$;
⑤ $4x^{4}-x^{2}+\frac{1}{4}$.
A.1 个
B.2 个
C.3 个
D.4 个
C
)① $x^{2}-10x + 25$;② $4a^{2}+4a - 1$;
③ $x^{2}-2x - 1$;④ $-m^{2}+m-\frac{1}{4}$;
⑤ $4x^{4}-x^{2}+\frac{1}{4}$.
A.1 个
B.2 个
C.3 个
D.4 个
答案:C.
解析:
① $x^{2}-10x + 25=(x-5)^{2}$,能用完全平方公式分解因式;
② $4a^{2}+4a - 1$,$4a^{2}=(2a)^{2}$,$-1$不是平方项,不能用完全平方公式分解因式;
③ $x^{2}-2x - 1$,$-1$不是平方项,不能用完全平方公式分解因式;
④ $-m^{2}+m-\frac{1}{4}=-(m^{2}-m+\frac{1}{4})=-(m-\frac{1}{2})^{2}$,能用完全平方公式分解因式;
⑤ $4x^{4}-x^{2}+\frac{1}{4}$,$(2x^{2})^{2}=4x^{4}$,$(\frac{1}{2})^{2}=\frac{1}{4}$,中间项应为$\pm 2× 2x^{2}× \frac{1}{2}=\pm 2x^{2}$,原式中间项是$-x^{2}$,不能用完全平方公式分解因式;
不能用完全平方公式分解因式的有②③⑤,共3个。
C.
② $4a^{2}+4a - 1$,$4a^{2}=(2a)^{2}$,$-1$不是平方项,不能用完全平方公式分解因式;
③ $x^{2}-2x - 1$,$-1$不是平方项,不能用完全平方公式分解因式;
④ $-m^{2}+m-\frac{1}{4}=-(m^{2}-m+\frac{1}{4})=-(m-\frac{1}{2})^{2}$,能用完全平方公式分解因式;
⑤ $4x^{4}-x^{2}+\frac{1}{4}$,$(2x^{2})^{2}=4x^{4}$,$(\frac{1}{2})^{2}=\frac{1}{4}$,中间项应为$\pm 2× 2x^{2}× \frac{1}{2}=\pm 2x^{2}$,原式中间项是$-x^{2}$,不能用完全平方公式分解因式;
不能用完全平方公式分解因式的有②③⑤,共3个。
C.
10. 已知 $a - b = 4$ 时,多项式 $ab + c^{2}$ 的值为 $-4$,则 $\frac{ab}{a^{2}+b^{2}+c^{2}}$ 的值为(
A.$-1$
B.$-\frac{1}{2}$
C.$-\frac{1}{3}$
D.0
B
)A.$-1$
B.$-\frac{1}{2}$
C.$-\frac{1}{3}$
D.0
答案:B.
解析:
已知$a - b = 4$,则$(a - b)^2 = 16$,即$a^2 - 2ab + b^2 = 16$,可得$a^2 + b^2 = 16 + 2ab$。
因为$ab + c^2 = -4$,所以$c^2 = -4 - ab$。
则$a^2 + b^2 + c^2 = (16 + 2ab) + (-4 - ab) = 12 + ab$。
所以$\frac{ab}{a^2 + b^2 + c^2} = \frac{ab}{12 + ab}$。
由$c^2 = -4 - ab \geq 0$,得$ab \leq -4$。
又因为$a^2 + b^2 = 16 + 2ab \geq 0$,即$ab \geq -8$,但结合$c^2$非负,$ab = -4 - c^2$,当$c = 0$时,$ab = -4$。
将$ab = -4$代入$\frac{ab}{12 + ab}$,得$\frac{-4}{12 + (-4)} = \frac{-4}{8} = -\frac{1}{2}$。
B.
因为$ab + c^2 = -4$,所以$c^2 = -4 - ab$。
则$a^2 + b^2 + c^2 = (16 + 2ab) + (-4 - ab) = 12 + ab$。
所以$\frac{ab}{a^2 + b^2 + c^2} = \frac{ab}{12 + ab}$。
由$c^2 = -4 - ab \geq 0$,得$ab \leq -4$。
又因为$a^2 + b^2 = 16 + 2ab \geq 0$,即$ab \geq -8$,但结合$c^2$非负,$ab = -4 - c^2$,当$c = 0$时,$ab = -4$。
将$ab = -4$代入$\frac{ab}{12 + ab}$,得$\frac{-4}{12 + (-4)} = \frac{-4}{8} = -\frac{1}{2}$。
B.