4. 计算:
(1)$\frac{4x^{2}-9}{2x - 1}÷\frac{1}{4x - 2}\cdot\frac{1}{2x - 3}$;
(2)$\frac{16 - m^{2}}{16 + 8m + m^{2}}÷\frac{m - 4}{2m + 8}\cdot\frac{m^{2}-4}{m + 2}$。
(1)$\frac{4x^{2}-9}{2x - 1}÷\frac{1}{4x - 2}\cdot\frac{1}{2x - 3}$;
(2)$\frac{16 - m^{2}}{16 + 8m + m^{2}}÷\frac{m - 4}{2m + 8}\cdot\frac{m^{2}-4}{m + 2}$。
答案:(1)$4x+6$;(2)$4-2m$.
解析:
(1)$\frac{4x^{2}-9}{2x - 1}÷\frac{1}{4x - 2}\cdot\frac{1}{2x - 3}$
$=\frac{(2x+3)(2x-3)}{2x-1}\cdot(4x-2)\cdot\frac{1}{2x-3}$
$=\frac{(2x+3)(2x-3)}{2x-1}\cdot2(2x-1)\cdot\frac{1}{2x-3}$
$=2(2x+3)$
$=4x+6$
(2)$\frac{16 - m^{2}}{16 + 8m + m^{2}}÷\frac{m - 4}{2m + 8}\cdot\frac{m^{2}-4}{m + 2}$
$=\frac{(4+m)(4-m)}{(4+m)^{2}}\cdot\frac{2(m+4)}{m-4}\cdot\frac{(m+2)(m-2)}{m+2}$
$=\frac{4-m}{4+m}\cdot\frac{2(m+4)}{m-4}\cdot(m-2)$
$=\frac{-(m-4)}{4+m}\cdot\frac{2(m+4)}{m-4}\cdot(m-2)$
$=-2(m-2)$
$=4-2m$
5. 已知$x - 3y = 0$,求$\frac{2x + y}{x^{2}-2xy + y^{2}}\cdot(x - y)$的值。
答案:原式$=\frac{2x+y}{(x-y)^2}\cdot(x-y)=\frac{2x+y}{x-y}$.当$x-3y=0$时,$x=3y$.原式$=\frac{6y+y}{3y-y}=\frac{7y}{2y}=\frac{7}{2}$.
6. 先化简,再求值:$\frac{x^{2}+2x + 1}{x^{2}-1}÷\frac{x^{2}+x}{x - 1}$,其中$x = 2$。
答案:原式$=\frac{1}{x}=\frac{1}{2}$.
解析:
原式$=\frac{(x+1)^2}{(x+1)(x-1)}\cdot\frac{x-1}{x(x+1)}$
$=\frac{x+1}{x-1}\cdot\frac{x-1}{x(x+1)}$
$=\frac{1}{x}$
当$x=2$时,原式$=\frac{1}{2}$
$=\frac{x+1}{x-1}\cdot\frac{x-1}{x(x+1)}$
$=\frac{1}{x}$
当$x=2$时,原式$=\frac{1}{2}$
7. 先化简,再求值:$\frac{81 - a^{2}}{a^{2}+6a + 9}÷\frac{9 - a}{2a + 6}\cdot\frac{1}{a + 9}$,其中$a = -5$。
答案:原式$=\frac{(9-a)(9+a)}{(a+3)^2}\cdot\frac{2(a+3)}{9-a}\cdot\frac{1}{a+9}=\frac{2}{a+3}$.当$a=-5$时,原式$=-1$.
8. 先化简,再求值:$\frac{a^{2}-b^{2}}{a^{2}}\cdot\frac{ab}{a^{2}-2ab + b^{2}}÷\frac{1}{ab - a^{2}}$,其中$a = \frac{1}{2}$,$b = -\frac{2}{3}$。
答案:原式$=-ab-b^2$,当$a=\frac{1}{2}$,$b=-\frac{2}{3}$时,原式$=-\frac{1}{9}$.
解析:
解:原式$=\frac{(a+b)(a-b)}{a^{2}}\cdot\frac{ab}{(a-b)^{2}}÷\frac{1}{a(b-a)}$
$=\frac{(a+b)(a-b)}{a^{2}}\cdot\frac{ab}{(a-b)^{2}}\cdot a(b-a)$
$=\frac{(a+b)(a-b)}{a^{2}}\cdot\frac{ab}{(a-b)^{2}}\cdot[-a(a-b)]$
$=-(a+b)b$
$=-ab - b^{2}$
当$a=\frac{1}{2}$,$b=-\frac{2}{3}$时,
原式$=-\frac{1}{2}×(-\frac{2}{3}) - (-\frac{2}{3})^{2}$
$=\frac{1}{3}-\frac{4}{9}$
$=-\frac{1}{9}$
$=\frac{(a+b)(a-b)}{a^{2}}\cdot\frac{ab}{(a-b)^{2}}\cdot a(b-a)$
$=\frac{(a+b)(a-b)}{a^{2}}\cdot\frac{ab}{(a-b)^{2}}\cdot[-a(a-b)]$
$=-(a+b)b$
$=-ab - b^{2}$
当$a=\frac{1}{2}$,$b=-\frac{2}{3}$时,
原式$=-\frac{1}{2}×(-\frac{2}{3}) - (-\frac{2}{3})^{2}$
$=\frac{1}{3}-\frac{4}{9}$
$=-\frac{1}{9}$
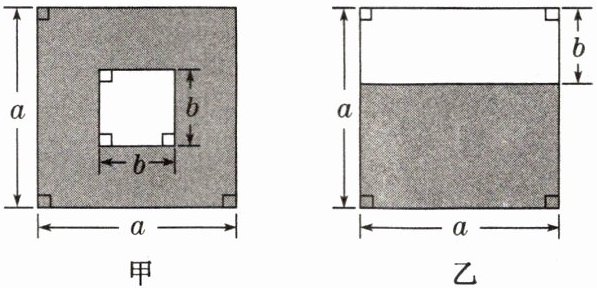
如图,设$k= \frac{甲图中阴影部分的面积}{乙图中阴影部分的面积}(a>b>0)$,则有(
 A. $k>2$
A. $k>2$
B. $1<k<2$
C. $\frac{1}{2}<k<1$
D. $0<k<\frac{1}{2}$
B
) A. $k>2$
A. $k>2$B. $1<k<2$
C. $\frac{1}{2}<k<1$
D. $0<k<\frac{1}{2}$
答案:B
解析:
甲图阴影面积:$a^2 - b^2$
乙图阴影面积:$a(a - b)$
$k = \frac{a^2 - b^2}{a(a - b)} = \frac{(a - b)(a + b)}{a(a - b)} = \frac{a + b}{a} = 1 + \frac{b}{a}$
$\because a > b > 0$,$\therefore 0 < \frac{b}{a} < 1$,$\therefore 1 < k < 2$
B
乙图阴影面积:$a(a - b)$
$k = \frac{a^2 - b^2}{a(a - b)} = \frac{(a - b)(a + b)}{a(a - b)} = \frac{a + b}{a} = 1 + \frac{b}{a}$
$\because a > b > 0$,$\therefore 0 < \frac{b}{a} < 1$,$\therefore 1 < k < 2$
B