如图是由三个小正方形组成的图形,请你在图中补画一个小正方形,使补画后的图形为轴对称图形。


答案:1. 在原图形左上角补画一个小正方形,使图形关于竖直对称轴对称。
2. 在原图形右上角补画一个小正方形,使图形关于竖直对称轴对称。
3. 在原图形下方两个小正方形的正下方中间位置补画一个小正方形,使图形关于水平对称轴对称。
2. 在原图形右上角补画一个小正方形,使图形关于竖直对称轴对称。
3. 在原图形下方两个小正方形的正下方中间位置补画一个小正方形,使图形关于水平对称轴对称。
1. 线段的垂直平分线是指经过线段
中点
并且垂直于
这条线段的直线.答案:中点,垂直于
2. 线段垂直平分线上的点与
这条线段两个端点的
距离相等.答案:这条线段两个端点的
3. 与线段
两个端点距离相等
的点在这条线段的垂直平分线上.答案:两个端点距离相等
4. 如果两个图形成轴对称,其对称轴就是
任何一对对称点
所连线段的垂直平分线.答案:任何一对对称点
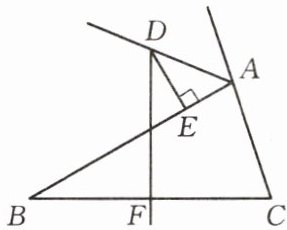
问题 如图,在△ABC中,AB>AC,BC的垂直平分线DF交△ABC的外角平分线AD于点D,DE⊥AB于点E. 求证:BE-AC= AE.
名师指导
要证明BE-AC= AE,用“截长补短法”,作DG⊥AC于点G,由角平分线的性质可知DG= DE及AG= AE. 为了证明BE= CG,可利用DF垂直平分BC,连接DB,DC,构造Rt△DBE≌Rt△DCG.
解题示范(学生在教师指导下,独立完成)
证明:

名师指导
要证明BE-AC= AE,用“截长补短法”,作DG⊥AC于点G,由角平分线的性质可知DG= DE及AG= AE. 为了证明BE= CG,可利用DF垂直平分BC,连接DB,DC,构造Rt△DBE≌Rt△DCG.
解题示范(学生在教师指导下,独立完成)
证明:
答案:证明:过点D作DG⊥AC,交CA的延长线于点G,连接DB、DC。
∵AD是△ABC的外角平分线,DE⊥AB,DG⊥AG,
∴DE=DG(角平分线上的点到角两边的距离相等)。
在Rt△ADE和Rt△ADG中,
∵AD=AD,DE=DG,
∴Rt△ADE≌Rt△ADG(HL)。
∴AE=AG。
∵DF是BC的垂直平分线,
∴DB=DC(线段垂直平分线上的点到线段两端点的距离相等)。
在Rt△DBE和Rt△DCG中,
∵DB=DC,DE=DG,
∴Rt△DBE≌Rt△DCG(HL)。
∴BE=CG。
∵点G在CA的延长线上,
∴CG=AC+AG。
∵AG=AE,
∴CG=AC+AE。
∵BE=CG,
∴BE=AC+AE。
∴BE-AC=AE。
∵AD是△ABC的外角平分线,DE⊥AB,DG⊥AG,
∴DE=DG(角平分线上的点到角两边的距离相等)。
在Rt△ADE和Rt△ADG中,
∵AD=AD,DE=DG,
∴Rt△ADE≌Rt△ADG(HL)。
∴AE=AG。
∵DF是BC的垂直平分线,
∴DB=DC(线段垂直平分线上的点到线段两端点的距离相等)。
在Rt△DBE和Rt△DCG中,
∵DB=DC,DE=DG,
∴Rt△DBE≌Rt△DCG(HL)。
∴BE=CG。
∵点G在CA的延长线上,
∴CG=AC+AG。
∵AG=AE,
∴CG=AC+AE。
∵BE=CG,
∴BE=AC+AE。
∴BE-AC=AE。