1. 到△ABC的三个顶点距离相等的点是△ABC的(
A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
D
)A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
答案:D
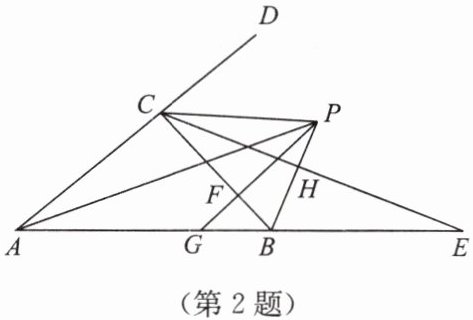
2. 如图,∠BAC与∠CBE的平分线相交于点P,BE= BC,PB与CE交于点H,PG//AD交BC于点F,交AB于点G. 有下列结论:①GA= GP;$②S_{△PAC}:S_{△PAB}= AC:AB;$③BP垂直平分CE;④FP= FC. 其中正确的结论有(
A.1个
B.2个
C.3个
D.4个
D
)
A.1个
B.2个
C.3个
D.4个
答案:D
解析:
证明:
①
∵AP平分∠BAC,
∴∠BAP=∠CAP.
∵PG//AD,
∴∠APG=∠CAP=∠BAP,
∴GA=GP.
②过P作PM⊥AC于M,PN⊥AB于N.
∵AP平分∠BAC,
∴PM=PN.
∵S△PAC=$\frac{1}{2}$AC·PM,S△PAB=$\frac{1}{2}$AB·PN,
∴S△PAC:S△PAB=AC:AB.
③
∵BP平分∠CBE,
∴∠CBP=∠EBP.
∵BE=BC,BP=BP,
∴△CBP≌△EBP(SAS),
∴CP=EP,BH=CH,
∴BP垂直平分CE.
④
∵PG//AD,
∴∠FPC=∠DCP.
∵CP平分∠ACD,
∴∠DCP=∠FCP,
∴∠FPC=∠FCP,
∴FP=FC.
综上,①②③④均正确,共4个.
答案:D
①
∵AP平分∠BAC,
∴∠BAP=∠CAP.
∵PG//AD,
∴∠APG=∠CAP=∠BAP,
∴GA=GP.
②过P作PM⊥AC于M,PN⊥AB于N.
∵AP平分∠BAC,
∴PM=PN.
∵S△PAC=$\frac{1}{2}$AC·PM,S△PAB=$\frac{1}{2}$AB·PN,
∴S△PAC:S△PAB=AC:AB.
③
∵BP平分∠CBE,
∴∠CBP=∠EBP.
∵BE=BC,BP=BP,
∴△CBP≌△EBP(SAS),
∴CP=EP,BH=CH,
∴BP垂直平分CE.
④
∵PG//AD,
∴∠FPC=∠DCP.
∵CP平分∠ACD,
∴∠DCP=∠FCP,
∴∠FPC=∠FCP,
∴FP=FC.
综上,①②③④均正确,共4个.
答案:D
3. 在△ABC中,AB= AC,BC= 10,AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,且DE= 4,则AD+AE的值为(
A.6
B.10
C.6或14
D.6或10
C
)A.6
B.10
C.6或14
D.6或10
答案:C
解析:
∵AB=AC,
∴△ABC是等腰三角形。
∵AB的垂直平分线交BC于D,
∴AD=BD。
∵AC的垂直平分线交BC于E,
∴AE=CE。
情况1:D在E左侧
∵BC=10,DE=4,
∴BD+CE=BC-DE=10-4=6,
∴AD+AE=BD+CE=6。
情况2:D在E右侧
∵BC=10,DE=4,
∴BD+CE=BC+DE=10+4=14,
∴AD+AE=BD+CE=14。
综上,AD+AE的值为6或14。
C
4. 如图,在△ABC中,边BC的垂直平分线DE交边BC于点D,交边AB于点E. 若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为
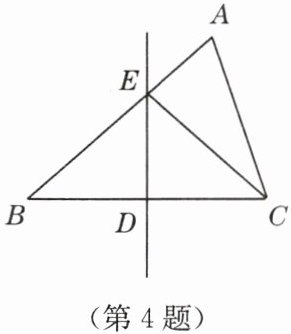
6
.
答案:6
解析:
证明:
∵DE是BC的垂直平分线,
∴BE=CE,BD=CD,设DE=x,CE=BE=a,CD=BD=b。
∵△EDC的周长为24,
∴DE+CE+CD=24,即x+a+b=24。①
∵△ABC与四边形AEDC的周长之差为12,
△ABC周长=AE+BE+BD+CD+AC,
四边形AEDC周长=AE+DE+CD+AC,
∴(AE+BE+BD+CD+AC)-(AE+DE+CD+AC)=12,
化简得BE+BD-DE=12,即a+b-x=12。②
①-②得:2x=12,解得x=6。
6
∵DE是BC的垂直平分线,
∴BE=CE,BD=CD,设DE=x,CE=BE=a,CD=BD=b。
∵△EDC的周长为24,
∴DE+CE+CD=24,即x+a+b=24。①
∵△ABC与四边形AEDC的周长之差为12,
△ABC周长=AE+BE+BD+CD+AC,
四边形AEDC周长=AE+DE+CD+AC,
∴(AE+BE+BD+CD+AC)-(AE+DE+CD+AC)=12,
化简得BE+BD-DE=12,即a+b-x=12。②
①-②得:2x=12,解得x=6。
6
5. 如图,在△ABC中,∠BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN⊥AB交AB的延长线于点N,PM⊥AC于点M. 求证:CM= BN.
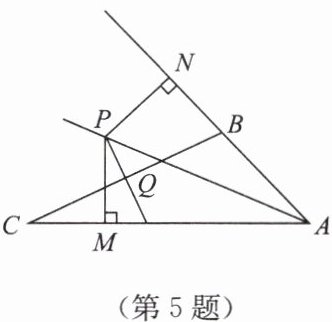

答案:证明:连接PB,PC.
∵ AP是∠BAC的平分线,PN⊥AB,PM⊥AC,
∴ PM=PN,∠PMC=∠PNB=90°.
∵ 点P在BC的垂直平分线上,
∴ PC=PB.在Rt△PMC和Rt△PNB中,{PC=PB,PM=PN},
∴ Rt△PMC≌Rt△PNB(HL).
∴ CM=BN
∵ AP是∠BAC的平分线,PN⊥AB,PM⊥AC,
∴ PM=PN,∠PMC=∠PNB=90°.
∵ 点P在BC的垂直平分线上,
∴ PC=PB.在Rt△PMC和Rt△PNB中,{PC=PB,PM=PN},
∴ Rt△PMC≌Rt△PNB(HL).
∴ CM=BN