1. 计算 $(-3x^{2}) \cdot 2x^{3}$ 的结果是 (
A.$-6x^{5}$
B.$-3x^{5}$
C.$2x^{5}$
D.$6x^{5}$
A
)A.$-6x^{5}$
B.$-3x^{5}$
C.$2x^{5}$
D.$6x^{5}$
答案:A
解析:
$(-3x^{2}) \cdot 2x^{3} = (-3 × 2) \cdot (x^{2} \cdot x^{3}) = -6x^{5}$,答案选A。
2. 下列运算中,计算错误的是 (
A.$2a \cdot 3a = 6a$
B.$(3a^{2})^{3} = 27a^{6}$
C.$3x^{2} \cdot 5x^{3} = 15x^{5}$
D.$\frac{1}{2}m \cdot 2m^{2} = m^{3}$
A
)A.$2a \cdot 3a = 6a$
B.$(3a^{2})^{3} = 27a^{6}$
C.$3x^{2} \cdot 5x^{3} = 15x^{5}$
D.$\frac{1}{2}m \cdot 2m^{2} = m^{3}$
答案:A
解析:
A选项:$2a \cdot 3a = 6a^{2}$,原计算错误;
B选项:$(3a^{2})^{3} = 27a^{6}$,计算正确;
C选项:$3x^{2} \cdot 5x^{3} = 15x^{5}$,计算正确;
D选项:$\frac{1}{2}m \cdot 2m^{2} = m^{3}$,计算正确。
答案:A
B选项:$(3a^{2})^{3} = 27a^{6}$,计算正确;
C选项:$3x^{2} \cdot 5x^{3} = 15x^{5}$,计算正确;
D选项:$\frac{1}{2}m \cdot 2m^{2} = m^{3}$,计算正确。
答案:A
3. 计算 $(-3x^{2}y) \cdot (\frac{1}{3}xy^{2}) = $
$-x^{3}y^{3}$
.答案:$-x^{3}y^{3}$
解析:
$(-3x^{2}y) \cdot (\frac{1}{3}xy^{2}) = (-3 × \frac{1}{3}) \cdot (x^{2} \cdot x) \cdot (y \cdot y^{2}) = -1 \cdot x^{3} \cdot y^{3} = -x^{3}y^{3}$
4. 如图,沿正方形的对角线对折,把对折后重合的两个小正方形内的单项式相乘,乘积是
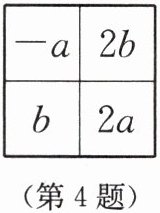
$2b^{2}$或$-2a^{2}$
(只需写出一个结论).
答案:$2b^{2}$或$-2a^{2}$
解析:
解:情况一:$-a × 2a = -2a^{2}$
情况二:$2b × b = 2b^{2}$
结论:$-2a^{2}$或$2b^{2}$
情况二:$2b × b = 2b^{2}$
结论:$-2a^{2}$或$2b^{2}$
5. 计算 $(-3a^{3})^{2} \cdot (-2a^{2})^{3} = $
$-72a^{12}$
.答案:$-72a^{12}$
解析:
$(-3a^{3})^{2} \cdot (-2a^{2})^{3}$
$=9a^{6} \cdot (-8a^{6})$
$=-72a^{12}$
$=9a^{6} \cdot (-8a^{6})$
$=-72a^{12}$
6. 计算:
(1) $-4mn^{3} \cdot 3mn^{2}$; (2) $-3a^{2}c \cdot (-2ab^{2})^{2}$;
(3) $3x \cdot (-4x^{2}y) \cdot 2y$; (4) $(4 × 10^{5}) × (5 × 10^{4})$.
(1) $-4mn^{3} \cdot 3mn^{2}$; (2) $-3a^{2}c \cdot (-2ab^{2})^{2}$;
(3) $3x \cdot (-4x^{2}y) \cdot 2y$; (4) $(4 × 10^{5}) × (5 × 10^{4})$.
答案:
(1)$-12m^{2}n^{5}$;
(2)$-12a^{4}b^{4}c$;
(3)$-24x^{3}y^{2}$;
(4)$2× 10^{10}$
(1)$-12m^{2}n^{5}$;
(2)$-12a^{4}b^{4}c$;
(3)$-24x^{3}y^{2}$;
(4)$2× 10^{10}$
7. 用 12 块边长为 $a$ 的正方形纸片拼成一个长方形,并用不同的方法表示你所拼出来的长方形的面积.你有几种不同的拼法?从不同的表示方法中,你能得到什么结论?
答案:共有三种拼法,面积总是$12a^{2}$
解析:
共有三种拼法:
1. 长为$12a$,宽为$a$,面积为$12a × a = 12a^{2}$;
2. 长为$6a$,宽为$2a$,面积为$6a × 2a = 12a^{2}$;
3. 长为$4a$,宽为$3a$,面积为$4a × 3a = 12a^{2}$。
结论:不同拼法得到的长方形面积相等,均为$12a^{2}$。
1. 长为$12a$,宽为$a$,面积为$12a × a = 12a^{2}$;
2. 长为$6a$,宽为$2a$,面积为$6a × 2a = 12a^{2}$;
3. 长为$4a$,宽为$3a$,面积为$4a × 3a = 12a^{2}$。
结论:不同拼法得到的长方形面积相等,均为$12a^{2}$。
8. 若 $(mx^{3}) \cdot (2x^{k}) = -8x^{18}$,求适合此等式的实数 $m$ 和 $k$ 的值.
答案:$m=-4$,$k=15$
解析:
$(mx^{3}) \cdot (2x^{k}) = 2m x^{3 + k}$,因为$(mx^{3}) \cdot (2x^{k}) = -8x^{18}$,所以$2m = -8$,$3 + k = 18$,解得$m = -4$,$k = 15$。