7. 先化简,再求值:$(x - 1)(x + 1)+(2x - 1)^{2}-2x(2x - 1)$,其中$x = 4$。
答案:原式$=x^2-1+4x^2-4x+1-4x^2+2x=x^2-2x$,把$x=4$代入,得原式$=4^2-2×4=16-8=8$.
解析:
解:原式$=(x^2 - 1) + (4x^2 - 4x + 1) - (4x^2 - 2x)$
$=x^2 - 1 + 4x^2 - 4x + 1 - 4x^2 + 2x$
$=x^2 - 2x$
当$x = 4$时,原式$=4^2 - 2×4 = 16 - 8 = 8$
$=x^2 - 1 + 4x^2 - 4x + 1 - 4x^2 + 2x$
$=x^2 - 2x$
当$x = 4$时,原式$=4^2 - 2×4 = 16 - 8 = 8$
8. 先化简,再求值:$(a - 2b)^{2}-(2a + b)(b - 2a)-4a(a - b)$,其中$a = -3$,$b = -1$。
答案:$a^2+3b^2$,12.
解析:
$(a - 2b)^{2}-(2a + b)(b - 2a)-4a(a - b)$
$=a^{2}-4ab + 4b^{2}-(b^{2}-4a^{2})-4a^{2}+4ab$
$=a^{2}-4ab + 4b^{2}-b^{2}+4a^{2}-4a^{2}+4ab$
$=a^{2}+3b^{2}$
当$a=-3$,$b=-1$时,
$a^{2}+3b^{2}=(-3)^{2}+3×(-1)^{2}=9 + 3×1=9 + 3=12$
$=a^{2}-4ab + 4b^{2}-(b^{2}-4a^{2})-4a^{2}+4ab$
$=a^{2}-4ab + 4b^{2}-b^{2}+4a^{2}-4a^{2}+4ab$
$=a^{2}+3b^{2}$
当$a=-3$,$b=-1$时,
$a^{2}+3b^{2}=(-3)^{2}+3×(-1)^{2}=9 + 3×1=9 + 3=12$
1. 如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“智慧数”。下列正整数中是“智慧数”的是(
A.$2022$
B.$2024$
C.$2026$
D.$2028$
D
)A.$2022$
B.$2024$
C.$2026$
D.$2028$
答案:D.
解析:
设两个连续偶数为$2n$和$2n+2$($n$为整数)。
$\begin{aligned}(2n+2)^2-(2n)^2&=(4n^2 + 8n + 4)-4n^2\\&=8n + 4\\&=4(2n + 1)\end{aligned}$
即智慧数是$4$的倍数且为$4$乘以奇数。
A. $2022÷4=505.5$,不是整数,不是智慧数。
B. $2024÷4=506$,$506$是偶数,不是智慧数。
C. $2026÷4=506.5$,不是整数,不是智慧数。
D. $2028÷4=507$,$507$是奇数,是智慧数。
D
$\begin{aligned}(2n+2)^2-(2n)^2&=(4n^2 + 8n + 4)-4n^2\\&=8n + 4\\&=4(2n + 1)\end{aligned}$
即智慧数是$4$的倍数且为$4$乘以奇数。
A. $2022÷4=505.5$,不是整数,不是智慧数。
B. $2024÷4=506$,$506$是偶数,不是智慧数。
C. $2026÷4=506.5$,不是整数,不是智慧数。
D. $2028÷4=507$,$507$是奇数,是智慧数。
D
2. 【动手操作】
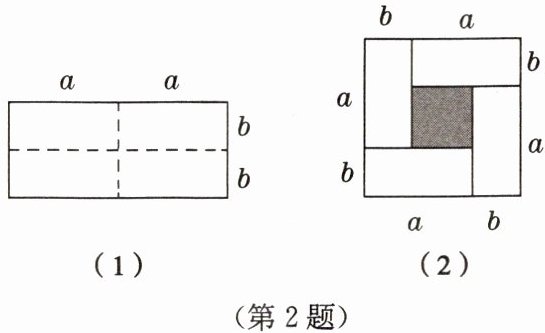
如图(1),有一个长为$2a$、宽为$2b$的长方形,沿图中的虚线将其剪开分成四个大小相等的长方形,然后按照图(2)所示拼成一个正方形。
【提出问题】
(1) 观察图(2),请用两种不同的方法表示阴影部分的面积:
(2) 请写出三个代数式$(a + b)^{2}$,$(a - b)^{2}$,$ab$之间的一个等量关系:
【问题解决】
(3) 根据上述(2)中得到的等量关系,解决下列问题:已知$x + y = 8$,$xy = 7$,求$x - y$的值。
]
如图(1),有一个长为$2a$、宽为$2b$的长方形,沿图中的虚线将其剪开分成四个大小相等的长方形,然后按照图(2)所示拼成一个正方形。
【提出问题】
(1) 观察图(2),请用两种不同的方法表示阴影部分的面积:
$(a-b)^2$
,$(a+b)^2-4ab$
。(2) 请写出三个代数式$(a + b)^{2}$,$(a - b)^{2}$,$ab$之间的一个等量关系:
$(a+b)^2-4ab=(a-b)^2$
。【问题解决】
(3) 根据上述(2)中得到的等量关系,解决下列问题:已知$x + y = 8$,$xy = 7$,求$x - y$的值。
]

(3)由(2),得$(x-y)^2=(x+y)^2-4xy$. $\because x+y=8$,$xy=7$,$\therefore (x-y)^2=64-28=36$,$\therefore x-y=\pm6$.
答案:(1)$(a-b)^2$,$(a+b)^2-4ab$;(2)$(a+b)^2-4ab=(a-b)^2$;(3)由(2),得$(x-y)^2=(x+y)^2-4xy$. $\because x+y=8$,$xy=7$,$\therefore (x-y)^2=64-28=36$,$\therefore x-y=\pm6$.