7. 设$a$,$b$是实数,定义$@$的一种运算如下:$a@b= (a + b)^{2}-(a - b)^{2}$,则下列结论:
(1) 若$a@b = 0$,则$a = 0或b = 0$;
(2) $a@(b + c)= a@b + a@c$;
(3) 不存在实数$a$,$b$,满足$a@b = a^{2}+5b^{2}$;
(4) 设$a$,$b$是矩形的长和宽,若矩形的周长固定,则当$a = b$时,$a@b$最大。
以上结论正确的有哪些?
(1) 若$a@b = 0$,则$a = 0或b = 0$;
(2) $a@(b + c)= a@b + a@c$;
(3) 不存在实数$a$,$b$,满足$a@b = a^{2}+5b^{2}$;
(4) 设$a$,$b$是矩形的长和宽,若矩形的周长固定,则当$a = b$时,$a@b$最大。
以上结论正确的有哪些?
答案:(1)(2)(4).
解析:
(1)$a@b=(a+b)^2-(a-b)^2=4ab$,若$a@b=0$,则$4ab=0$,即$a=0$或$b=0$,正确;
(2)$a@(b+c)=4a(b+c)=4ab+4ac=a@b+a@c$,正确;
(3)$a@b=4ab=a^2+5b^2$,即$a^2-4ab+5b^2=0$,$(a-2b)^2+b^2=0$,则$a=2b=0$,存在$a=b=0$满足,错误;
(4)设周长为$2C$,则$a+b=C$,$a@b=4ab=4a(C-a)=-4(a-\frac{C}{2})^2+C^2$,当$a=b=\frac{C}{2}$时,$a@b$最大,正确。
(1)(2)(4)
(2)$a@(b+c)=4a(b+c)=4ab+4ac=a@b+a@c$,正确;
(3)$a@b=4ab=a^2+5b^2$,即$a^2-4ab+5b^2=0$,$(a-2b)^2+b^2=0$,则$a=2b=0$,存在$a=b=0$满足,错误;
(4)设周长为$2C$,则$a+b=C$,$a@b=4ab=4a(C-a)=-4(a-\frac{C}{2})^2+C^2$,当$a=b=\frac{C}{2}$时,$a@b$最大,正确。
(1)(2)(4)
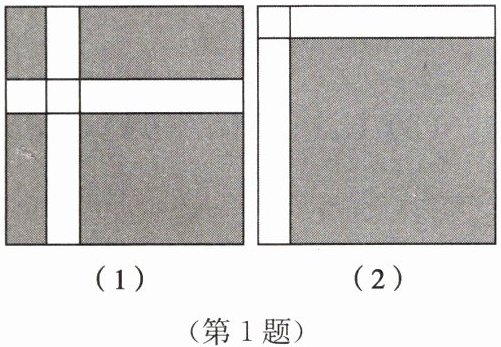
1. 如图(1),在边长为$a$米的正方形草坪上修建两条宽为$b$米的道路。
(1) 为了求得剩余草坪的面积,小明同学想出了两种方法。
方法①:用正方形面积减道路面积;
方法②:将道路平移到如图(2)所示的位置。
请你根据小明的两种求面积的方法,直接写出含有字母$a$,$b$的代数式表示的等式:
(2) 根据(1)中的等式,解决如下问题:
① 已知$a - b = 5$,$a^{2}+b^{2}= 20$,求$ab$的值;
② 已知$(x - 2023)^{2}+(x - 2025)^{2}= 12$,求$(x - 2024)^{2}$的值。
]
(1) 为了求得剩余草坪的面积,小明同学想出了两种方法。
方法①:用正方形面积减道路面积;
方法②:将道路平移到如图(2)所示的位置。
请你根据小明的两种求面积的方法,直接写出含有字母$a$,$b$的代数式表示的等式:
$(a-b)^2=a^2-2ab+b^2$
。(2) 根据(1)中的等式,解决如下问题:
① 已知$a - b = 5$,$a^{2}+b^{2}= 20$,求$ab$的值;
② 已知$(x - 2023)^{2}+(x - 2025)^{2}= 12$,求$(x - 2024)^{2}$的值。
]

① 把$a-b=5$,$a^2+b^2=20$代入$(a-b)^2=a^2-2ab+b^2$,$\therefore 5^2=20-2ab$,$\therefore ab=-2.5$. ② 5.
答案:(1)$(a-b)^2=a^2-2ab+b^2$;(2)① 把$a-b=5$,$a^2+b^2=20$代入$(a-b)^2=a^2-2ab+b^2$,$\therefore 5^2=20-2ab$,$\therefore ab=-2.5$. ② 5.
解析:
(1)$(a-b)^2=a^2-2ab+b^2$
(2)① 把$a-b=5$,$a^2+b^2=20$代入$(a-b)^2=a^2-2ab+b^2$,得$5^2=20-2ab$,解得$ab=-\frac{5}{2}$
② 设$y=x-2024$,则$(x-2023)=y+1$,$(x-2025)=y-1$,原方程化为$(y+1)^2+(y-1)^2=12$,展开得$y^2+2y+1+y^2-2y+1=12$,即$2y^2+2=12$,$2y^2=10$,$y^2=5$,故$(x-2024)^2=5$
(2)① 把$a-b=5$,$a^2+b^2=20$代入$(a-b)^2=a^2-2ab+b^2$,得$5^2=20-2ab$,解得$ab=-\frac{5}{2}$
② 设$y=x-2024$,则$(x-2023)=y+1$,$(x-2025)=y-1$,原方程化为$(y+1)^2+(y-1)^2=12$,展开得$y^2+2y+1+y^2-2y+1=12$,即$2y^2+2=12$,$2y^2=10$,$y^2=5$,故$(x-2024)^2=5$
2. 已知$a$,$b$,$c为\triangle ABC$的三边长,且$2a^{2}+2b^{2}+2c^{2}= 2ab + 2ac + 2bc$,试判断$\triangle ABC$的形状,并证明你的结论。
答案:$\triangle ABC$是等边三角形. 证明如下:$\because 2a^2+2b^2+2c^2=2ab+2ac+2bc$,$\therefore 2a^2+2b^2+2c^2-2ab-2ac-2bc=0$,即$a^2-2ab+b^2+a^2-2ac+c^2+b^2-2bc+c^2=0$,$\therefore (a-b)^2+(a-c)^2+(b-c)^2=0$,$\therefore a-b=0$,$a-c=0$,$b-c=0$,得$a=b$,$a=c$,$b=c$,即$a=b=c$,所以$\triangle ABC$是等边三角形.