10. (2024·湖北)铁的密度约为 $ 7.9 \, g/cm^{3} $,铁块的质量 $ m $ (单位:$ g $) 与它的体积 $ V $ (单位:$ cm^{3} $) 之间的函数关系式为 $ m = 7.9V $,当 $ V = 10 \, cm^{3} $ 时,$ m = $
79
$ g $。答案:79
11. 一辆汽车的油箱中现有汽油 $ 50 \, L $,如果不再加油,那么油箱中的油量 $ y(L) $ 随行驶里程 $ x(km) $ 的增加而减少,平均耗油量是 $ 0.1 \, L/km $。
(1) 写出 $ y $ 与 $ x $ 的函数关系式;
(2) 指出自变量 $ x $ 的取值范围;
(3) 汽车行驶 $ 200 \, km $ 时,油箱中还有多少升汽油?
(1) 写出 $ y $ 与 $ x $ 的函数关系式;
(2) 指出自变量 $ x $ 的取值范围;
(3) 汽车行驶 $ 200 \, km $ 时,油箱中还有多少升汽油?
答案:解:
(1)y=50-0.1x.
(2)0≤x≤500.
(3)将 x=200 代入 y=50-0.1x 中,得 y=30. 故油箱中还有 30 L 汽油.
(1)y=50-0.1x.
(2)0≤x≤500.
(3)将 x=200 代入 y=50-0.1x 中,得 y=30. 故油箱中还有 30 L 汽油.
12. 如图,在靠墙(墙长 $ 18 $ 米) 的地方围成一个长方形养鸡场,另三边用篱笆围成,如果篱笆长 $ 35 $ 米,求养鸡场的长 $ y $ (米) 与宽 $ x $ (米) $ (y > x) $ 之间的函数表达式,并写出自变量 $ x $ 的取值范围。
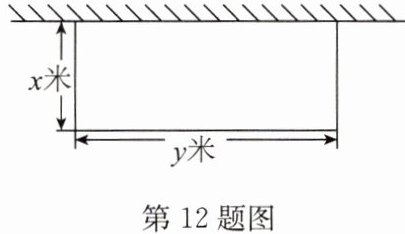

答案:解:y=35-2x,其中 $\frac{17}{2} \leqslant x < \frac{35}{3}$.
解析:
解:由题意得,$y + 2x = 35$,则$y = 35 - 2x$。
因为$y > x$,所以$35 - 2x > x$,解得$x < \frac{35}{3}$。
又因为墙长$18$米,所以$y \leq 18$,即$35 - 2x \leq 18$,解得$x \geq \frac{17}{2}$。
且$x > 0$,综上,自变量$x$的取值范围是$\frac{17}{2} \leq x < \frac{35}{3}$。
故养鸡场的长$y$与宽$x$之间的函数表达式为$y = 35 - 2x$,自变量$x$的取值范围是$\frac{17}{2} \leq x < \frac{35}{3}$。
因为$y > x$,所以$35 - 2x > x$,解得$x < \frac{35}{3}$。
又因为墙长$18$米,所以$y \leq 18$,即$35 - 2x \leq 18$,解得$x \geq \frac{17}{2}$。
且$x > 0$,综上,自变量$x$的取值范围是$\frac{17}{2} \leq x < \frac{35}{3}$。
故养鸡场的长$y$与宽$x$之间的函数表达式为$y = 35 - 2x$,自变量$x$的取值范围是$\frac{17}{2} \leq x < \frac{35}{3}$。
13. 如图,正方形 $ ABCD $ 的边长为 $ 1 $,$ E $ 是 $ CD $ 的中点,$ P $ 为正方形 $ ABCD $ 边上一个动点,动点 $ P $ 从点 $ A $ 出发,沿 $ A \to B \to C \to E $ 运动,到达点 $ E $。若点 $ P $ 经过的路程为 $ x $,$ \triangle APE $ 的面积为 $ y $,则当 $ y = \frac{1}{3} $ 时,求 $ x $ 的值。
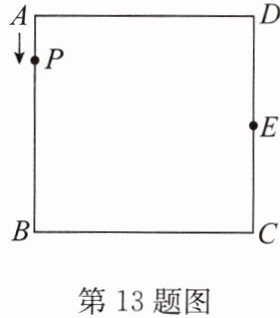

答案:解:①当点 P 在 AB 边上时,0≤x<1,$y=\frac{1}{2}x$. 当$y=\frac{1}{3}$时,有$\frac{1}{3}=\frac{1}{2}x$,解得$x=\frac{2}{3}$. ②当点 P 在 BC 边上时,1≤x<2. $y=1-\frac{1}{2}(x-1)-\frac{1}{2}×\frac{1}{2}(2-x)-\frac{1}{4}=\frac{3}{4}-\frac{1}{4}x$. 当$y=\frac{1}{3}$时,有$\frac{1}{3}=\frac{3}{4}-\frac{1}{4}x$,解得$x=\frac{5}{3}$. ③当点 P 在线段 CE 上时,2≤x≤2.5. $y=\frac{1}{2}×1×(\frac{5}{2}-x)=\frac{5}{4}-\frac{1}{2}x$. 当$y=\frac{1}{3}$时,有$\frac{1}{3}=\frac{5}{4}-\frac{1}{2}x$,解得$x=\frac{11}{6}$. $\because \frac{11}{6}$不在 2≤x≤2.5 内,$\therefore$此情况不符合要求. 综上可知,x 的值为$\frac{2}{3}$或$\frac{5}{3}$.
解析:
解:①当点P在AB边上时,$0 \leq x < 1$,$y = \frac{1}{2}x$。
当$y = \frac{1}{3}$时,$\frac{1}{3} = \frac{1}{2}x$,解得$x = \frac{2}{3}$。
②当点P在BC边上时,$1 \leq x < 2$,$y = \frac{3}{4} - \frac{1}{4}x$。
当$y = \frac{1}{3}$时,$\frac{1}{3} = \frac{3}{4} - \frac{1}{4}x$,解得$x = \frac{5}{3}$。
③当点P在线段CE上时,$2 \leq x \leq 2.5$,$y = \frac{5}{4} - \frac{1}{2}x$。
当$y = \frac{1}{3}$时,$\frac{1}{3} = \frac{5}{4} - \frac{1}{2}x$,解得$x = \frac{11}{6}$。
$\because \frac{11}{6}$不在$2 \leq x \leq 2.5$内,$\therefore$此情况不符合要求。
综上,$x$的值为$\frac{2}{3}$或$\frac{5}{3}$。
当$y = \frac{1}{3}$时,$\frac{1}{3} = \frac{1}{2}x$,解得$x = \frac{2}{3}$。
②当点P在BC边上时,$1 \leq x < 2$,$y = \frac{3}{4} - \frac{1}{4}x$。
当$y = \frac{1}{3}$时,$\frac{1}{3} = \frac{3}{4} - \frac{1}{4}x$,解得$x = \frac{5}{3}$。
③当点P在线段CE上时,$2 \leq x \leq 2.5$,$y = \frac{5}{4} - \frac{1}{2}x$。
当$y = \frac{1}{3}$时,$\frac{1}{3} = \frac{5}{4} - \frac{1}{2}x$,解得$x = \frac{11}{6}$。
$\because \frac{11}{6}$不在$2 \leq x \leq 2.5$内,$\therefore$此情况不符合要求。
综上,$x$的值为$\frac{2}{3}$或$\frac{5}{3}$。