8. 已知 $y - 3$ 与 $2x - 1$ 成正比例,且当 $x = 1$ 时,$y = 6$.
(1)求 $y$ 与 $x$ 之间的函数表达式;
(2)已知点 $P(m,n)$ 在该函数的图象上,且 $m - n = 4$,求点 $P$ 的坐标.
(1)求 $y$ 与 $x$ 之间的函数表达式;
(2)已知点 $P(m,n)$ 在该函数的图象上,且 $m - n = 4$,求点 $P$ 的坐标.
答案:解:
(1)$\because y-3$与$2x-1$成正比例,
∴设$y-3=k(2x-1).$$\because$当$x=1$时,$y=6,\therefore 6-3=k(2×1-1).$$\therefore k=3,\therefore y-3=3(2x-1)$,即$y=6x.$
∴y与x之间的函数表达式为$y=6x.$
(2)由题意得$\left\{\begin{array}{l} n=6m,\\ m-n=4\end{array}\right. $解得$\left\{\begin{array}{l} m=-\frac {4}{5},\\ n=-\frac {24}{5}.\end{array}\right. $$\therefore P(-\frac {4}{5},-\frac {24}{5}).$
(1)$\because y-3$与$2x-1$成正比例,
∴设$y-3=k(2x-1).$$\because$当$x=1$时,$y=6,\therefore 6-3=k(2×1-1).$$\therefore k=3,\therefore y-3=3(2x-1)$,即$y=6x.$
∴y与x之间的函数表达式为$y=6x.$
(2)由题意得$\left\{\begin{array}{l} n=6m,\\ m-n=4\end{array}\right. $解得$\left\{\begin{array}{l} m=-\frac {4}{5},\\ n=-\frac {24}{5}.\end{array}\right. $$\therefore P(-\frac {4}{5},-\frac {24}{5}).$
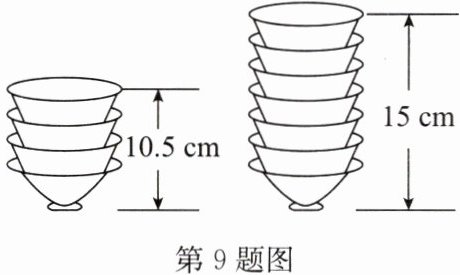
9. 如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题.
(1)若摆放在桌面上的饭碗的高度 $y(cm)$ 与饭碗个数 $x$ 符合一次函数关系,求 $y$ 与 $x$ 之间的函数表达式;
(2)把这两摞饭碗整齐地摆成一摞时,这摞饭碗的高度是多少厘米?
(1)若摆放在桌面上的饭碗的高度 $y(cm)$ 与饭碗个数 $x$ 符合一次函数关系,求 $y$ 与 $x$ 之间的函数表达式;
(2)把这两摞饭碗整齐地摆成一摞时,这摞饭碗的高度是多少厘米?

答案:解:
(1)设$y=kx+b(k≠0).$由题图可知,当$x=4$时,$y=10.5;$当$x=7$时,$y=15.$将其分别代入$y=kx+b$,得$\left\{\begin{array}{l} 10.5=4k+b,\\ 15=7k+b\end{array}\right. $解得$\left\{\begin{array}{l} k=1.5,\\ b=4.5.\end{array}\right. $所以y与x之间的函数表达式是$y=1.5x+4.5$(x是正整数).
(2)当$x=4+7=11$时,$y=1.5×11+4.5=21.$即把这两摞饭碗整齐地摆成一摞时,这摞饭碗的高度是21cm.
(1)设$y=kx+b(k≠0).$由题图可知,当$x=4$时,$y=10.5;$当$x=7$时,$y=15.$将其分别代入$y=kx+b$,得$\left\{\begin{array}{l} 10.5=4k+b,\\ 15=7k+b\end{array}\right. $解得$\left\{\begin{array}{l} k=1.5,\\ b=4.5.\end{array}\right. $所以y与x之间的函数表达式是$y=1.5x+4.5$(x是正整数).
(2)当$x=4+7=11$时,$y=1.5×11+4.5=21.$即把这两摞饭碗整齐地摆成一摞时,这摞饭碗的高度是21cm.
10. 我国航天事业发展迅速,2023 年 5 月 30 日 9 时 31 分,神舟十六号载人飞船成功发射. 某玩具店抓住商机,先购进了 $1000$ 件相关航天模型玩具进行试销,进价为 $50$ 元/件.
(1)设每件玩具的售价为 $x$ 元,全部售完的利润为 $y$ 元. 求利润 $y(元)$ 关于售价 $x(元/件)$ 的函数表达式;
(2)当售价定为 $60$ 元/件时,该玩具销售火爆,该店继续购进一批该种航天模型玩具,并从中拿出这两批玩具销售利润的 $20\%$ 用于支持某航模兴趣组开展活动,在成功销售完毕后,资助经费恰好是 $10000$ 元,请问该商店继续购进了多少件航天模型玩具?
(1)设每件玩具的售价为 $x$ 元,全部售完的利润为 $y$ 元. 求利润 $y(元)$ 关于售价 $x(元/件)$ 的函数表达式;
(2)当售价定为 $60$ 元/件时,该玩具销售火爆,该店继续购进一批该种航天模型玩具,并从中拿出这两批玩具销售利润的 $20\%$ 用于支持某航模兴趣组开展活动,在成功销售完毕后,资助经费恰好是 $10000$ 元,请问该商店继续购进了多少件航天模型玩具?
答案:解:
(1)$y=1000(x-50)=1000x-50000.$
(2)设该商店继续购进了m件航天模型玩具.$(60-50)(1000+m)×20\% =10000$,解得$m=4000.$答:该商店继续购进了4000件航天模型玩具.
(1)$y=1000(x-50)=1000x-50000.$
(2)设该商店继续购进了m件航天模型玩具.$(60-50)(1000+m)×20\% =10000$,解得$m=4000.$答:该商店继续购进了4000件航天模型玩具.