1. 下列说法中,正确的是 (
A.周长相等的两个直角三角形全等
B.周长相等的两个钝角三角形全等
C.周长相等的两个等腰三角形全等
D.周长相等的两个等边三角形全等
D
)A.周长相等的两个直角三角形全等
B.周长相等的两个钝角三角形全等
C.周长相等的两个等腰三角形全等
D.周长相等的两个等边三角形全等
答案:D
2. 如图,在$\triangle ABC$中,已知$AB = AC$,$AD\perp BC$,且$BC = 4$,则$BD$的长为 (

A.1
B.2
C.3
D.4
B
)
A.1
B.2
C.3
D.4
答案:B
解析:
∵在△ABC中,AB=AC,AD⊥BC,
∴AD是△ABC底边BC上的中线(等腰三角形底边上的高、底边上的中线、顶角平分线互相重合),
∵BC=4,
∴BD=$\frac{1}{2}$BC=$\frac{1}{2}×4$=2。
答案:B
3. (2024·云南)已知$AF是等腰\triangle ABC底边BC$上的高,若点$F到直线AB的距离为3$,则点$F到直线AC$的距离为 (
A.$\frac{3}{2}$
B.2
C.3
D.$\frac{7}{2}$
C
)A.$\frac{3}{2}$
B.2
C.3
D.$\frac{7}{2}$
答案:C
解析:
∵AF是等腰△ABC底边BC上的高,
∴AB=AC,∠BAF=∠CAF,
∴点F在∠BAC的平分线上,
∵角平分线上的点到角两边的距离相等,点F到直线AB的距离为3,
∴点F到直线AC的距离为3。
C
4. (2024·福建)小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案,如图.其中$\triangle OAB与\triangle ODC$都是等腰三角形,且它们关于直线$l$对称,$E,F分别是底边AB,CD$的中点,$OE\perp OF$.下列推断错误的是 (

A.$OB\perp OD$
B.$\angle BOC= \angle AOB$
C.$OE = OF$
D.$\angle BOC+\angle AOD = 180^{\circ}$
B
)
A.$OB\perp OD$
B.$\angle BOC= \angle AOB$
C.$OE = OF$
D.$\angle BOC+\angle AOD = 180^{\circ}$
答案:B
解析:
∵△OAB与△ODC关于直线l对称,
∴△OAB≌△ODC,OE=OF,∠AOE=∠DOF,∠BOE=∠COF,故C正确;
∵E,F分别是底边AB,CD的中点,△OAB与△ODC是等腰三角形,
∴OE⊥AB,OF⊥CD,
∵OE⊥OF,
∴∠EOF=90°,即∠EOB+∠BOF=90°,
∵∠BOF=∠BOE+∠EOF=∠BOE+90°,∠COD=2∠COF=2∠BOE,
∴∠BOD=∠BOF+∠FOD=∠BOE+90°+∠AOE=∠AOB+90°,无法得出OB⊥OD,故A错误;
∵∠AOB=2∠AOE,∠BOC=∠BOE+∠COF=2∠BOE,由于∠AOE不一定等于∠BOE,
∴∠BOC不一定等于∠AOB,故B错误;
∵∠AOD=∠AOE+∠EOF+∠FOD=2∠AOE+90°,∠BOC=2∠BOE,
∴∠AOD+∠BOC=2(∠AOE+∠BOE)+90°=2∠AOB+90°,无法得出∠BOC+∠AOD=180°,故D错误。
综上,推断错误的是B。
答案:B
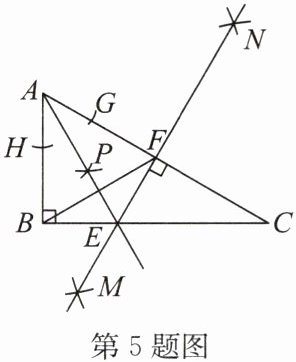
5. (2024·泰安)如图,$Rt\triangle ABC$中,$\angle ABC = 90^{\circ}$,分别以顶点$A,C$为圆心,大
A.1个
B.2个
C.3个
D.4个
于
$\frac{1}{2}AC$长为半径画弧,两弧分别相交于点$M和点N$,作直线$MN$,分别与$BC,AC交于点E和点F$;以点$A$为圆心,任意长为半径画弧,分别交$AB,AC于点H和点G$,再分别以点$H,G$为圆心,大于$\frac{1}{2}HG$长为半径画弧,两弧交于点$P$,作射线$AP$,若射线$AP恰好经过点E$,则下列四个结论:①$\angle C = 30^{\circ}$;②$AP垂直平分线段BF$;③$CE = 2BE$;④$S_{\triangle BEF}= \frac{1}{6}S_{\triangle ABC}$.其中,正确的结论有 (D
)
A.1个
B.2个
C.3个
D.4个
答案:D
解析:
证明:
1. 由作图知,MN垂直平分AC,AP平分∠BAC。设∠BAE=∠CAE=α,则∠BAC=2α,∠C=90°-2α。
∵MN垂直平分AC,
∴EA=EC,∠EAC=∠C=90°-2α。
又∠EAC=α,
∴α=90°-2α,解得α=30°,∠C=30°,①正确。
2.
∵∠BAC=60°,MN垂直平分AC,F为AC中点,BF=AF=CF。
AP平分∠BAC,∠BAE=30°,∠ABC=90°,∠AEB=60°。
∵BF=AF,∠BAF=60°,△ABF为等边三角形,AP⊥BF且平分BF,②正确。
3. 设BE=x,∠BAE=30°,AB=√3 x,AE=2x=EC。
∵∠C=30°,BC=AB·√3=3x,CE=BC-BE=2x,即CE=2BE,③正确。
4. 设BE=x,AB=√3 x,BC=3x,S△ABC=1/2·AB·BC=3√3/2 x²。
F为AC中点,BF=1/2 AC=√3 x,EF=BE=x,S△BEF=1/2·BE·EF·sin60°=√3/4 x²=1/6 S△ABC,④正确。
结论:①②③④均正确,选D。
D
1. 由作图知,MN垂直平分AC,AP平分∠BAC。设∠BAE=∠CAE=α,则∠BAC=2α,∠C=90°-2α。
∵MN垂直平分AC,
∴EA=EC,∠EAC=∠C=90°-2α。
又∠EAC=α,
∴α=90°-2α,解得α=30°,∠C=30°,①正确。
2.
∵∠BAC=60°,MN垂直平分AC,F为AC中点,BF=AF=CF。
AP平分∠BAC,∠BAE=30°,∠ABC=90°,∠AEB=60°。
∵BF=AF,∠BAF=60°,△ABF为等边三角形,AP⊥BF且平分BF,②正确。
3. 设BE=x,∠BAE=30°,AB=√3 x,AE=2x=EC。
∵∠C=30°,BC=AB·√3=3x,CE=BC-BE=2x,即CE=2BE,③正确。
4. 设BE=x,AB=√3 x,BC=3x,S△ABC=1/2·AB·BC=3√3/2 x²。
F为AC中点,BF=1/2 AC=√3 x,EF=BE=x,S△BEF=1/2·BE·EF·sin60°=√3/4 x²=1/6 S△ABC,④正确。
结论:①②③④均正确,选D。
D
6. 已知一等腰三角形的一个内角为$80^{\circ}$,则这个等腰三角形顶角的度数为
20°或80°
.答案:20°或80°
解析:
情况一:当$80^{\circ}$角为顶角时,顶角的度数为$80^{\circ}$。
情况二:当$80^{\circ}$角为底角时,顶角的度数为$180^{\circ}-80^{\circ}×2=20^{\circ}$。
$20^{\circ}$或$80^{\circ}$
情况二:当$80^{\circ}$角为底角时,顶角的度数为$180^{\circ}-80^{\circ}×2=20^{\circ}$。
$20^{\circ}$或$80^{\circ}$
7. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AM平分\angle BAC$,$CM = 4\ cm$,$AB = 7\ cm$,则$\triangle ABM$的面积是

14
$cm^2$.
答案:14
解析:
解:过点$M$作$MD \perp AB$于点$D$。
因为$AM$平分$\angle BAC$,$\angle C = 90^{\circ}$,$MD \perp AB$,
所以$MD = CM = 4\ cm$。
$\triangle ABM$的面积为$\dfrac{1}{2} × AB × MD = \dfrac{1}{2} × 7 × 4 = 14\ cm^2$。
14
因为$AM$平分$\angle BAC$,$\angle C = 90^{\circ}$,$MD \perp AB$,
所以$MD = CM = 4\ cm$。
$\triangle ABM$的面积为$\dfrac{1}{2} × AB × MD = \dfrac{1}{2} × 7 × 4 = 14\ cm^2$。
14
8. (2024·宿城期末)如图,在$\triangle ABC$中,$AB = AD = CD$,且$\angle C = 40^{\circ}$,则$\angle BAD$的度数为

20°
.
答案:20°
解析:
解:在$\triangle ADC$中,$AD=CD$,$\angle C=40^{\circ}$,
$\therefore \angle DAC=\angle C=40^{\circ}$,
$\angle ADC=180^{\circ}-\angle DAC-\angle C=180^{\circ}-40^{\circ}-40^{\circ}=100^{\circ}$,
$\angle ADB=180^{\circ}-\angle ADC=180^{\circ}-100^{\circ}=80^{\circ}$,
在$\triangle ABD$中,$AB=AD$,
$\therefore \angle B=\angle ADB=80^{\circ}$,
$\angle BAD=180^{\circ}-\angle B-\angle ADB=180^{\circ}-80^{\circ}-80^{\circ}=20^{\circ}$。
20°
$\therefore \angle DAC=\angle C=40^{\circ}$,
$\angle ADC=180^{\circ}-\angle DAC-\angle C=180^{\circ}-40^{\circ}-40^{\circ}=100^{\circ}$,
$\angle ADB=180^{\circ}-\angle ADC=180^{\circ}-100^{\circ}=80^{\circ}$,
在$\triangle ABD$中,$AB=AD$,
$\therefore \angle B=\angle ADB=80^{\circ}$,
$\angle BAD=180^{\circ}-\angle B-\angle ADB=180^{\circ}-80^{\circ}-80^{\circ}=20^{\circ}$。
20°