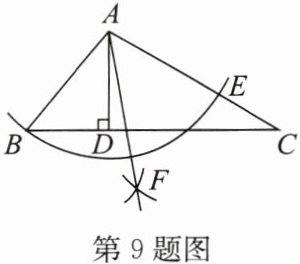
9. (2024·宿迁)如图,在$\triangle ABC$中,$\angle B = 50^{\circ}$,$\angle C = 30^{\circ}$,$AD$是高,以点$A$为圆心,$AB$长为半径画弧,交$AC于点E$,再分别以点$B,E$为圆心,大于$\frac{1}{2}BE$长为半径画弧,两弧在$\angle BAC的内部交于点F$,作射线$AF$,则$\angle DAF= $
10
$^{\circ}$.
答案:10
解析:
解:在$\triangle ABC$中,$\angle BAC=180^{\circ}-\angle B-\angle C=180^{\circ}-50^{\circ}-30^{\circ}=100^{\circ}$。
AD是高,$\angle ADB=90^{\circ}$,则$\angle BAD=90^{\circ}-\angle B=90^{\circ}-50^{\circ}=40^{\circ}$。
以A为圆心,AB长为半径画弧交AC于E,得AE=AB。
由作图知AF是$\angle BAC$的平分线,$\angle BAF=\frac{1}{2}\angle BAC=\frac{1}{2}×100^{\circ}=50^{\circ}$。
$\angle DAF=\angle BAF-\angle BAD=50^{\circ}-40^{\circ}=10^{\circ}$。
10
AD是高,$\angle ADB=90^{\circ}$,则$\angle BAD=90^{\circ}-\angle B=90^{\circ}-50^{\circ}=40^{\circ}$。
以A为圆心,AB长为半径画弧交AC于E,得AE=AB。
由作图知AF是$\angle BAC$的平分线,$\angle BAF=\frac{1}{2}\angle BAC=\frac{1}{2}×100^{\circ}=50^{\circ}$。
$\angle DAF=\angle BAF-\angle BAD=50^{\circ}-40^{\circ}=10^{\circ}$。
10
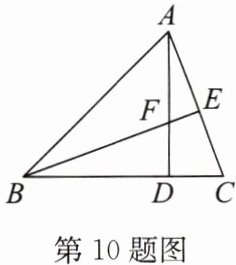
10. 如图,在$\triangle ABC$中,$AD是BC$边上的高,$BE是AC$边上的高,且$AD,BE交于点F$.若$BF = AC$,$CD = 3$,$BD = 8$,则线段$AF$的长度为
5
.
答案:5
解析:
证明:
∵AD是BC边上的高,BE是AC边上的高,
∴∠ADB=∠ADC=∠BEC=90°。
∵∠BFD=∠AFE,∠AFE+∠CAD=90°,∠CAD+∠C=90°,
∴∠BFD=∠C。
在△BDF和△ADC中,
$\left\{\begin{array}{l} ∠BDF=∠ADC=90° \\ ∠BFD=∠C \\ BF=AC \end{array}\right.$,
∴△BDF≌△ADC(AAS)。
∴BD=AD=8,DF=CD=3。
∵AD=AF+DF,
∴AF=AD-DF=8-3=5。
5
∵AD是BC边上的高,BE是AC边上的高,
∴∠ADB=∠ADC=∠BEC=90°。
∵∠BFD=∠AFE,∠AFE+∠CAD=90°,∠CAD+∠C=90°,
∴∠BFD=∠C。
在△BDF和△ADC中,
$\left\{\begin{array}{l} ∠BDF=∠ADC=90° \\ ∠BFD=∠C \\ BF=AC \end{array}\right.$,
∴△BDF≌△ADC(AAS)。
∴BD=AD=8,DF=CD=3。
∵AD=AF+DF,
∴AF=AD-DF=8-3=5。
5
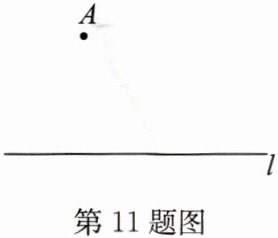
11. (15分)(2024·陕西)如图,已知直线$l和l外一点A$,请用尺规作图法,求作一个等腰直角$\triangle ABC$,使得顶点$B和顶点C都在直线l$上.(作出符合题意的一个等腰直角三角形即可,保留作图痕迹,不写作法)

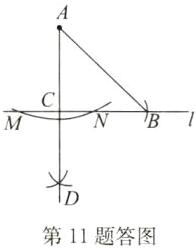
答案:
解:如答图,△ABC即为所求作的三角形.(答案不唯一)
解:如答图,△ABC即为所求作的三角形.(答案不唯一)

12. (15分)(2024·宜宾)如图,$D,E分别是等边三角形ABC的边BC,AC$上的点,且$BD = CE$,$BE与AD交于点F$.求证:$AD = BE$.
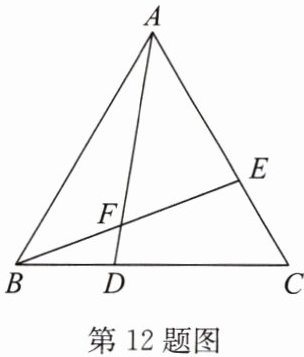

答案:证明:
∵△ABC为等边三角形,
∴∠ABD=∠C=60°,AB=BC;在△ABD和△BCE中,$\left\{\begin{array}{l} AB=BC,\\ ∠ABD=∠C,\\ BD=CE,\end{array}\right. $
∴△ABD≌△BCE(SAS),
∴AD=BE.
∵△ABC为等边三角形,
∴∠ABD=∠C=60°,AB=BC;在△ABD和△BCE中,$\left\{\begin{array}{l} AB=BC,\\ ∠ABD=∠C,\\ BD=CE,\end{array}\right. $
∴△ABD≌△BCE(SAS),
∴AD=BE.
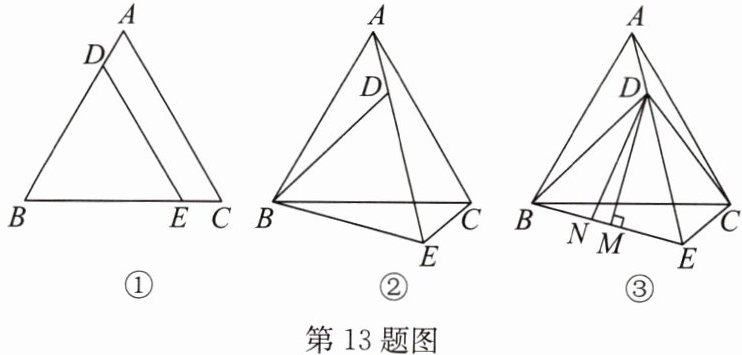
13. (20分)(2024·宿迁共同体期末)如图①,$\triangle ABC$是等边三角形,点$D,E分别在边AB,BC$上,且$BD = BE$,连接$DE$.
(1)求证:$DE// AC$;
(2)将图①中的$\triangle BDE绕点B$顺时针旋转,使得点$A,D,E$在同一条直线上,如图②,求$\angle AEC$的度数;
(3)在(2)的条件下,如图③,连接$CD$,过点$D作DM\perp BE于点M$,在线段$BM上取点N$,使得$\angle DNE+\angle DCE = 180^{\circ}$.求证:$EN - EC = 2MN$.
(1)求证:$DE// AC$;
(2)将图①中的$\triangle BDE绕点B$顺时针旋转,使得点$A,D,E$在同一条直线上,如图②,求$\angle AEC$的度数;
(3)在(2)的条件下,如图③,连接$CD$,过点$D作DM\perp BE于点M$,在线段$BM上取点N$,使得$\angle DNE+\angle DCE = 180^{\circ}$.求证:$EN - EC = 2MN$.

答案:
(1)证明:
∵△ABC是等边三角形,
∴∠B=∠C=60°.
又
∵BD=BE,
∴△BDE是等边三角形,
∴∠BED=60°,
∴∠C=∠BED,
∴DE//AC;
(2)解:
∵△ABC、△BDE都是等边三角形,
∴BA=BC,BD=BE,∠ABC=∠DBE=∠BDE=∠BED=60°,
∴∠ABD=∠CBE.
在△ABD和△CBE中,$\left\{\begin{array}{l} BA=BC,\\ ∠ABD=∠CBE,\\ BD=BE,\end{array}\right. $
∴△ABD≌△CBE(SAS),
∴∠CEB=∠ADB.
∵∠ADB=180°−∠BDE=180°−60°=120°,
∴∠CEB=120°.
∴∠AEC=∠CEB−∠BED=120°−60°=60°.
(3)证明:
∵∠DNE+∠DCE=180°,∠DNE+∠DNB=180°,
∴∠DCE=∠DNB.
由
(1)知△BDE是等边三角形,
∴BD=ED,∠DBE=60°.
由
(2)知∠AEC=60°,
∴∠DBN=∠DEC.
在△BDN和△EDC中,$\left\{\begin{array}{l} ∠DBN=∠DEC,\\ ∠DNB=∠DCE,\\ BD=ED,\end{array}\right. $
∴△BDN≌△EDC(AAS),
∴BN=EC.
∵DB=DE,DM⊥BE,
∴BM=EM,即BN+MN=EN−MN;
∴CE+MN=EN−MN,
∴EN−EC=2MN.
(1)证明:
∵△ABC是等边三角形,
∴∠B=∠C=60°.
又
∵BD=BE,
∴△BDE是等边三角形,
∴∠BED=60°,
∴∠C=∠BED,
∴DE//AC;
(2)解:
∵△ABC、△BDE都是等边三角形,
∴BA=BC,BD=BE,∠ABC=∠DBE=∠BDE=∠BED=60°,
∴∠ABD=∠CBE.
在△ABD和△CBE中,$\left\{\begin{array}{l} BA=BC,\\ ∠ABD=∠CBE,\\ BD=BE,\end{array}\right. $
∴△ABD≌△CBE(SAS),
∴∠CEB=∠ADB.
∵∠ADB=180°−∠BDE=180°−60°=120°,
∴∠CEB=120°.
∴∠AEC=∠CEB−∠BED=120°−60°=60°.
(3)证明:
∵∠DNE+∠DCE=180°,∠DNE+∠DNB=180°,
∴∠DCE=∠DNB.
由
(1)知△BDE是等边三角形,
∴BD=ED,∠DBE=60°.
由
(2)知∠AEC=60°,
∴∠DBN=∠DEC.
在△BDN和△EDC中,$\left\{\begin{array}{l} ∠DBN=∠DEC,\\ ∠DNB=∠DCE,\\ BD=ED,\end{array}\right. $
∴△BDN≌△EDC(AAS),
∴BN=EC.
∵DB=DE,DM⊥BE,
∴BM=EM,即BN+MN=EN−MN;
∴CE+MN=EN−MN,
∴EN−EC=2MN.