1. (2024·福建)下列各数中,无理数是(
A.$-3$
B.$0$
C.$\frac{2}{3}$
D.$\sqrt{5}$
D
)A.$-3$
B.$0$
C.$\frac{2}{3}$
D.$\sqrt{5}$
答案:D
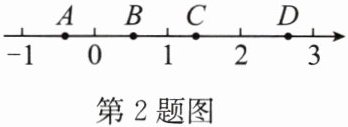
2. (2024·南充)如图,数轴上表示$\sqrt{2}$的点可能是(
A.点$A$
B.点$B$
C.点$C$
D.点$D$
C
)
A.点$A$
B.点$B$
C.点$C$
D.点$D$
答案:C
解析:
解:因为$1^2 = 1$,$2^2 = 4$,所以$1 < \sqrt{2} < 2$。由数轴可知,点$C$在$1$和$2$之间,故表示$\sqrt{2}$的点可能是点$C$。
C
C
3. (2024·宿迁共同体期末)在数:$0.23$,$16$,$2\pi$,$\sqrt{2}$,$\frac{1}{3}$,$-\sqrt[3]{49}$,$0.2020020002…$(相邻两个$2之间0的个数逐次加1$)中,无理数有(
A.$5$个
B.$4$个
C.$3$个
D.$2$个
B
)A.$5$个
B.$4$个
C.$3$个
D.$2$个
答案:B
解析:
无理数是无限不循环小数。
$0.23$是有限小数,不是无理数;
$16$是整数,不是无理数;
$2\pi$,$\pi$是无限不循环小数,故$2\pi$是无理数;
$\sqrt{2}$是开方开不尽的数,是无理数;
$\frac{1}{3}$是无限循环小数,不是无理数;
$-\sqrt[3]{49}$是开方开不尽的数,是无理数;
$0.2020020002…$(相邻两个$2$之间$0$的个数逐次加$1$)是无限不循环小数,是无理数。
综上,无理数有$2\pi$,$\sqrt{2}$,$-\sqrt[3]{49}$,$0.2020020002…$,共$4$个。
B
$0.23$是有限小数,不是无理数;
$16$是整数,不是无理数;
$2\pi$,$\pi$是无限不循环小数,故$2\pi$是无理数;
$\sqrt{2}$是开方开不尽的数,是无理数;
$\frac{1}{3}$是无限循环小数,不是无理数;
$-\sqrt[3]{49}$是开方开不尽的数,是无理数;
$0.2020020002…$(相邻两个$2$之间$0$的个数逐次加$1$)是无限不循环小数,是无理数。
综上,无理数有$2\pi$,$\sqrt{2}$,$-\sqrt[3]{49}$,$0.2020020002…$,共$4$个。
B
4. 写出一个大于$-1$的负无理数:
√2 - 2(答案不唯一)
.答案:√2 - 2(答案不唯一)
解析:
$\sqrt{2}-2$
5. 把下列各数写入相应的集合中:$-\frac{1}{2}$,$\sqrt[3]{9}$,$0$,$1$,$\frac{\pi}{2}$,$\sqrt{36}$,$\sqrt[3]{-27}$,$0.0.1212212221…$(相邻两个$1之间2的个数逐次加1$).
(1) 正实数集合:…{ $$ };
(2) 分数集合:…{ $$ };
(3) 有理数集合:…{ $$ };
(4) 无理数集合:…{ $$ }.
(1) 正实数集合:…{ $$ };
(2) 分数集合:…{ $$ };
(3) 有理数集合:…{ $$ };
(4) 无理数集合:…{ $$ }.
答案:
(1)$\sqrt[3]{9}$,$0.1$,$\frac{\pi}{2}$,$\sqrt{36}$,$0.1212212221…$(相邻两个$1之间2的个数逐次加1$);
(2)$-\frac{1}{2}$,$0.1$;
(3)$-\frac{1}{2}$,$0.1$,$\sqrt{36}$,$\sqrt[3]{-27}$,$0$;
(4)$\sqrt[3]{9}$,$\frac{\pi}{2}$,$0.1212212221…$(相邻两个$1之间2的个数逐次加1$)
(1)$\sqrt[3]{9}$,$0.1$,$\frac{\pi}{2}$,$\sqrt{36}$,$0.1212212221…$(相邻两个$1之间2的个数逐次加1$);
(2)$-\frac{1}{2}$,$0.1$;
(3)$-\frac{1}{2}$,$0.1$,$\sqrt{36}$,$\sqrt[3]{-27}$,$0$;
(4)$\sqrt[3]{9}$,$\frac{\pi}{2}$,$0.1212212221…$(相邻两个$1之间2的个数逐次加1$)
6. (2024·临夏州)下列各数中,是无理数的是(
A.$\frac{\pi}{2}$
B.$\frac{1}{3}$
C.$\sqrt[3]{27}$
D.$0.13133$
A
)A.$\frac{\pi}{2}$
B.$\frac{1}{3}$
C.$\sqrt[3]{27}$
D.$0.13133$
答案:A
7. 若$\sqrt{a}是大于2且小于3$的无理数,则$a$的值可以是
5(答案不唯一)
.(填一个合适的即可)答案:5(答案不唯一)
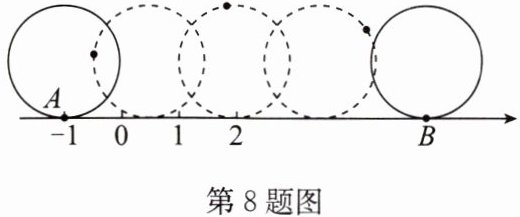
8. 如图,半径为$1个单位长度的圆沿数轴从数-1$对应的点向右滚动一周,圆上的点$A恰好与点B$重合,则点$B$对应的数是
$2\pi - 1$
.(结果保留$\pi$)
答案:$2\pi - 1$
解析:
解:圆的半径为1,其周长为$2\pi r = 2\pi×1 = 2\pi$。
点A初始位置对应的数为-1,圆向右滚动一周,点A移动的距离为圆的周长$2\pi$,所以点B对应的数是$-1 + 2\pi = 2\pi - 1$。
$2\pi - 1$
点A初始位置对应的数为-1,圆向右滚动一周,点A移动的距离为圆的周长$2\pi$,所以点B对应的数是$-1 + 2\pi = 2\pi - 1$。
$2\pi - 1$
9. 任何一个无限循环小数都可以写成分数的形式,应该怎样写呢?我们以无限循环小数$0.\dot{7}$为例进行说明:设$0.\dot{7}= x$.由$0.\dot{7}= 0.777…$可知,$10x= 7.777…$,所以$10x-x= 7$,解方程得$x= \frac{7}{9}$,于是,得$0.\dot{7}= \frac{7}{9}$.仿照例子,将$0.\dot{3}\dot{6}$写成分数的形式是
$\frac{4}{11}$
.答案:$\frac{4}{11}$
解析:
设$0.\dot{3}\dot{6}=x$。由$0.\dot{3}\dot{6}=0.363636\ldots$可知,$100x=36.363636\ldots$,所以$100x - x=36$,即$99x=36$,解方程得$x=\frac{36}{99}=\frac{4}{11}$。于是,得$0.\dot{3}\dot{6}=\frac{4}{11}$。