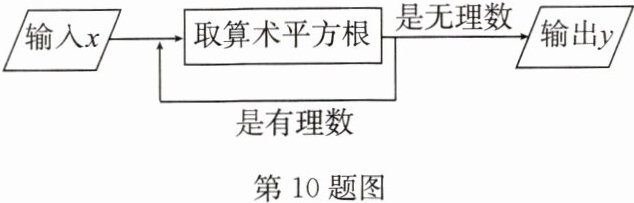
10. 一个数值转换器的原理如图所示,当输入的$x是256$时,$y= $
$\sqrt{2}$
.
答案:$\sqrt{2}$
解析:
解:当输入$x = 256$时,
$\sqrt{256} = 16$,16是有理数;
输入$x = 16$时,
$\sqrt{16} = 4$,4是有理数;
输入$x = 4$时,
$\sqrt{4} = 2$,2是有理数;
输入$x = 2$时,
$\sqrt{2}$是无理数,
$\therefore y = \sqrt{2}$
$\sqrt{2}$
$\sqrt{256} = 16$,16是有理数;
输入$x = 16$时,
$\sqrt{16} = 4$,4是有理数;
输入$x = 4$时,
$\sqrt{4} = 2$,2是有理数;
输入$x = 2$时,
$\sqrt{2}$是无理数,
$\therefore y = \sqrt{2}$
$\sqrt{2}$
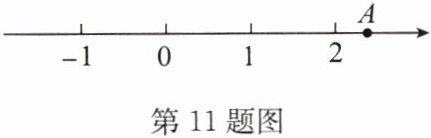
11. 如图,点$A是数轴上表示数a$的点.
(1) 用直尺和圆规在数轴上作出表示数$\sqrt{2}的点P$;(保留作图痕迹,不写作法)
(2) 利用数轴比较$\sqrt{2}和a$的大小,并说明理由.
(1) 用直尺和圆规在数轴上作出表示数$\sqrt{2}的点P$;(保留作图痕迹,不写作法)
(2) 利用数轴比较$\sqrt{2}和a$的大小,并说明理由.

答案:
解:
(1)如答图所示,点P即为所求.
(2)$a>\sqrt{2}$.理由:如答图,点A在点P的右侧,
∴$a>\sqrt{2}$.

解:
(1)如答图所示,点P即为所求.
(2)$a>\sqrt{2}$.理由:如答图,点A在点P的右侧,
∴$a>\sqrt{2}$.

12. 先阅读材料,然后解答提出的问题:
如果两个数相等,那么有理数部分与有理数部分相等,无理数部分与无理数部分相等.例如,$a$,$b$是有理数,且满足$a+\sqrt{2}b= 3-5\sqrt{2}$,则$a= 3$,$b= -5$.
问题:设$x$,$y$是有理数,且$x$,$y满足等式x^{2}+2y+\sqrt{3}y= 17-4\sqrt{3}$,求$xy$的值.
如果两个数相等,那么有理数部分与有理数部分相等,无理数部分与无理数部分相等.例如,$a$,$b$是有理数,且满足$a+\sqrt{2}b= 3-5\sqrt{2}$,则$a= 3$,$b= -5$.
问题:设$x$,$y$是有理数,且$x$,$y满足等式x^{2}+2y+\sqrt{3}y= 17-4\sqrt{3}$,求$xy$的值.
答案:解:
∵$x,y$是有理数,且$x,y$满足等式$x^{2}+2y+\sqrt{3}y=17 - 4\sqrt{3}$,
∴$\begin{cases} x^{2}+2y=17, \\ y=-4, \end{cases}$解得$\begin{cases} x=5, \\ y=-4 \end{cases}$或$\begin{cases} x=-5, \\ y=-4. \end{cases}$当$x = 5,y = - 4$时,$xy = - 20$;当$x = - 5,y = - 4$时,$xy = 20$.
∵$x,y$是有理数,且$x,y$满足等式$x^{2}+2y+\sqrt{3}y=17 - 4\sqrt{3}$,
∴$\begin{cases} x^{2}+2y=17, \\ y=-4, \end{cases}$解得$\begin{cases} x=5, \\ y=-4 \end{cases}$或$\begin{cases} x=-5, \\ y=-4. \end{cases}$当$x = 5,y = - 4$时,$xy = - 20$;当$x = - 5,y = - 4$时,$xy = 20$.
13. 我们知道$\sqrt{2}$是无理数,因此$\sqrt{2}$的小数部分我们不可能全部写出来,于是小明用$\sqrt{2}-1来表示\sqrt{2}$的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为$\sqrt{2}的整数部分是1$,将这个数减去其整数部分,差就是小数部分.又例如$\sqrt{4}<\sqrt{5}<\sqrt{9}$,即$2<\sqrt{5}<3$,所以$\sqrt{5}的整数部分为2$,小数部分为$\sqrt{5}-2$.请根据以上信息,回答下列问题:
(1)$\sqrt{34}$的整数部分是
(2) 如果$\sqrt{11}的整数部分为a$,$7-\sqrt{7}的整数部分为b$,求$12a+7b$的立方根.
(1)$\sqrt{34}$的整数部分是
5
,小数部分是______$\sqrt{34}-5$
;(2) 如果$\sqrt{11}的整数部分为a$,$7-\sqrt{7}的整数部分为b$,求$12a+7b$的立方根.
答案:
(1)5 $\sqrt{34}-5$
(2)解:
∵$\sqrt{9}<\sqrt{11}<\sqrt{16}$即$3<\sqrt{11}<4$,
∴$\sqrt{11}$的整数部分为3,
∴$a = 3$.
∵$7 - \sqrt{7}=4 + 3 - \sqrt{7}$,$7 - \sqrt{7}$的整数部分为$b$,
∴$b = 4$,
∴$12a + 7b=12×3 + 7×4=36 + 28 = 64$.
∴$12a + 7b$的立方根为$\sqrt[3]{64}=4$.
(1)5 $\sqrt{34}-5$
(2)解:
∵$\sqrt{9}<\sqrt{11}<\sqrt{16}$即$3<\sqrt{11}<4$,
∴$\sqrt{11}$的整数部分为3,
∴$a = 3$.
∵$7 - \sqrt{7}=4 + 3 - \sqrt{7}$,$7 - \sqrt{7}$的整数部分为$b$,
∴$b = 4$,
∴$12a + 7b=12×3 + 7×4=36 + 28 = 64$.
∴$12a + 7b$的立方根为$\sqrt[3]{64}=4$.