1.(2024·威海)下列各数中,最小的数是(
A.$-2$
B.$-(-2)$
C.$-\frac{1}{2}$
D.$-\sqrt{2}$
A
)A.$-2$
B.$-(-2)$
C.$-\frac{1}{2}$
D.$-\sqrt{2}$
答案:A
2. $\sqrt{4}$的平方根是(
A.$\pm 2$
B.$2$
C.$\sqrt{2}$
D.$\pm \sqrt{2}$
D
)A.$\pm 2$
B.$2$
C.$\sqrt{2}$
D.$\pm \sqrt{2}$
答案:D
解析:
$\sqrt{4}=2$,2的平方根是$\pm \sqrt{2}$,故答案为D。
3.(2024·宿迁共同体期末)若$m= \sqrt{40}-4$,则估计$m$的值所在的范围是(
A.$1<m<2$
B.$2<m<3$
C.$3<m<4$
D.$4<m<5$
B
)A.$1<m<2$
B.$2<m<3$
C.$3<m<4$
D.$4<m<5$
答案:B
解析:
因为$36 < 40 < 49$,所以$\sqrt{36} < \sqrt{40} < \sqrt{49}$,即$6 < \sqrt{40} < 7$。
不等式两边同时减$4$,得$6 - 4 < \sqrt{40} - 4 < 7 - 4$,即$2 < m < 3$。
B
不等式两边同时减$4$,得$6 - 4 < \sqrt{40} - 4 < 7 - 4$,即$2 < m < 3$。
B
4. 某种鲸鱼的体重约是$1.36×10^{5}$kg,关于这个近似数,下列说法正确的是(
A.精确到百分位
B.精确到$0.01$
C.精确到百位
D.精确到千位
D
)A.精确到百分位
B.精确到$0.01$
C.精确到百位
D.精确到千位
答案:D
解析:
$1.36×10^{5} = 136000$,6在千位,所以精确到千位。
D
D
5. $16$的平方根是
±4
;0.16
的算术平方根是$0.4$;$\frac{1}{1000}$的立方根是$\frac{1}{10}$
.答案:±4 0.16 $\frac{1}{10}$
6. 写出比$\sqrt{2}大且比\sqrt{15}$小的整数:
2,3
.答案:2,3
7.(2024·包头)计算:$\sqrt[3]{8}+(-1)^{2024}= $
3
.答案:3
解析:
$\sqrt[3]{8}=2$,$(-1)^{2024}=1$,$2+1=3$
8. 如图,数轴上表示$3$,$\sqrt{13}的对应点分别为C$,$B$.$C是线段AB$的中点,则点$A$表示的数是
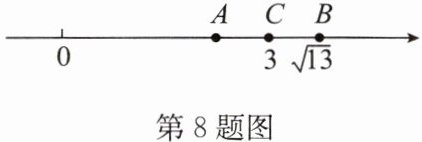
$6-\sqrt{13}$
.
答案:$6-\sqrt{13}$
解析:
解:设点$A$表示的数是$x$。
因为$C$是线段$AB$的中点,点$C$表示的数是$3$,点$B$表示的数是$\sqrt{13}$,
所以$\frac{x + \sqrt{13}}{2}=3$,
解得$x=6-\sqrt{13}$。
$6-\sqrt{13}$
因为$C$是线段$AB$的中点,点$C$表示的数是$3$,点$B$表示的数是$\sqrt{13}$,
所以$\frac{x + \sqrt{13}}{2}=3$,
解得$x=6-\sqrt{13}$。
$6-\sqrt{13}$
9. 将$5个边长为1$的正方形拼在一起,形成如图所示的长方形,通过剪一剪、拼一拼,该长方形可以拼成一个面积相同的大正方形,则大正方形的边长等于
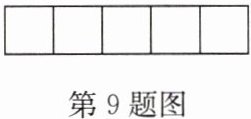
$\sqrt{5}$
.
答案:$\sqrt{5}$
解析:
长方形面积为$5×1×1 = 5$,大正方形面积等于长方形面积,设大正方形边长为$a$,则$a^2=5$,解得$a = \sqrt{5}$。
$\sqrt{5}$
$\sqrt{5}$
10.(16分)计算.
(1)$(\pi -3.14)^{0}-\sqrt[3]{27}+(\sqrt{5})^{2}$;
(2)$|-\sqrt{4}|-(\frac{1}{3})^{-1}+2025^{0}$;
(3)$\sqrt[3]{216}-\sqrt[3]{-3-\frac{3}{8}}×\sqrt{400}$;
(4)$(-\sqrt{2})^{2}+\sqrt{(-6)^{2}}-\sqrt[3]{-27}$.
(1)$(\pi -3.14)^{0}-\sqrt[3]{27}+(\sqrt{5})^{2}$;
(2)$|-\sqrt{4}|-(\frac{1}{3})^{-1}+2025^{0}$;
(3)$\sqrt[3]{216}-\sqrt[3]{-3-\frac{3}{8}}×\sqrt{400}$;
(4)$(-\sqrt{2})^{2}+\sqrt{(-6)^{2}}-\sqrt[3]{-27}$.
答案:1. (1)
解:
根据零指数幂公式$a^{0}=1(a\neq0)$,可得$(\pi - 3.14)^{0}=1$;
根据立方根公式$\sqrt[3]{a^{3}}=a$,$\sqrt[3]{27}=\sqrt[3]{3^{3}} = 3$;
根据二次根式性质$(\sqrt{a})^{2}=a(a\geq0)$,$(\sqrt{5})^{2}=5$。
则$(\pi - 3.14)^{0}-\sqrt[3]{27}+(\sqrt{5})^{2}=1 - 3+5=3$。
2. (2)
解:
根据绝对值性质$\vert-\sqrt{4}\vert=\vert - 2\vert = 2$;
根据负整数指数幂公式$a^{-p}=\frac{1}{a^{p}}(a\neq0,p\in N^{*})$,$(\frac{1}{3})^{-1}=3$;
根据零指数幂公式$a^{0}=1(a\neq0)$,$2025^{0}=1$。
则$\vert-\sqrt{4}\vert-(\frac{1}{3})^{-1}+2025^{0}=2 - 3 + 1=0$。
3. (3)
解:
根据立方根公式$\sqrt[3]{216}=\sqrt[3]{6^{3}} = 6$;
先计算$-3-\frac{3}{8}=-\frac{24 + 3}{8}=-\frac{27}{8}$,则$\sqrt[3]{-3-\frac{3}{8}}=\sqrt[3]{-\frac{27}{8}}=-\frac{3}{2}$;
根据二次根式性质$\sqrt{400}=\sqrt{20^{2}} = 20$。
所以$\sqrt[3]{216}-\sqrt[3]{-3-\frac{3}{8}}×\sqrt{400}=6-(-\frac{3}{2})×20$
$=6 + 30=36$。
4. (4)
解:
根据二次根式性质$(-\sqrt{2})^{2}=2$;
$\sqrt{(-6)^{2}}=\vert - 6\vert = 6$;
根据立方根公式$\sqrt[3]{-27}=\sqrt[3]{(-3)^{3}}=-3$。
则$(-\sqrt{2})^{2}+\sqrt{(-6)^{2}}-\sqrt[3]{-27}=2 + 6-(-3)=2 + 6 + 3=11$。
综上,答案依次为:(1)$3$;(2)$0$;(3)$36$;(4)$11$。
解:
根据零指数幂公式$a^{0}=1(a\neq0)$,可得$(\pi - 3.14)^{0}=1$;
根据立方根公式$\sqrt[3]{a^{3}}=a$,$\sqrt[3]{27}=\sqrt[3]{3^{3}} = 3$;
根据二次根式性质$(\sqrt{a})^{2}=a(a\geq0)$,$(\sqrt{5})^{2}=5$。
则$(\pi - 3.14)^{0}-\sqrt[3]{27}+(\sqrt{5})^{2}=1 - 3+5=3$。
2. (2)
解:
根据绝对值性质$\vert-\sqrt{4}\vert=\vert - 2\vert = 2$;
根据负整数指数幂公式$a^{-p}=\frac{1}{a^{p}}(a\neq0,p\in N^{*})$,$(\frac{1}{3})^{-1}=3$;
根据零指数幂公式$a^{0}=1(a\neq0)$,$2025^{0}=1$。
则$\vert-\sqrt{4}\vert-(\frac{1}{3})^{-1}+2025^{0}=2 - 3 + 1=0$。
3. (3)
解:
根据立方根公式$\sqrt[3]{216}=\sqrt[3]{6^{3}} = 6$;
先计算$-3-\frac{3}{8}=-\frac{24 + 3}{8}=-\frac{27}{8}$,则$\sqrt[3]{-3-\frac{3}{8}}=\sqrt[3]{-\frac{27}{8}}=-\frac{3}{2}$;
根据二次根式性质$\sqrt{400}=\sqrt{20^{2}} = 20$。
所以$\sqrt[3]{216}-\sqrt[3]{-3-\frac{3}{8}}×\sqrt{400}=6-(-\frac{3}{2})×20$
$=6 + 30=36$。
4. (4)
解:
根据二次根式性质$(-\sqrt{2})^{2}=2$;
$\sqrt{(-6)^{2}}=\vert - 6\vert = 6$;
根据立方根公式$\sqrt[3]{-27}=\sqrt[3]{(-3)^{3}}=-3$。
则$(-\sqrt{2})^{2}+\sqrt{(-6)^{2}}-\sqrt[3]{-27}=2 + 6-(-3)=2 + 6 + 3=11$。
综上,答案依次为:(1)$3$;(2)$0$;(3)$36$;(4)$11$。