7. (2024·宿迁共同体期末)已知直角三角形的两条直角边长$a$,$b满足\sqrt{a - 3}+\vert4 - b\vert=0$,则第三条边的长为
5
。答案:5
解析:
因为$\sqrt{a - 3} \geq 0$,$\vert4 - b\vert \geq 0$,且$\sqrt{a - 3}+\vert4 - b\vert=0$,所以$\sqrt{a - 3}=0$,$\vert4 - b\vert=0$。
由$\sqrt{a - 3}=0$,得$a - 3=0$,即$a=3$;由$\vert4 - b\vert=0$,得$4 - b=0$,即$b=4$。
因为直角三角形的两条直角边长为$a=3$,$b=4$,根据勾股定理,第三条边(斜边)的长为$\sqrt{a^2 + b^2}=\sqrt{3^2 + 4^2}=\sqrt{9 + 16}=\sqrt{25}=5$。
5
由$\sqrt{a - 3}=0$,得$a - 3=0$,即$a=3$;由$\vert4 - b\vert=0$,得$4 - b=0$,即$b=4$。
因为直角三角形的两条直角边长为$a=3$,$b=4$,根据勾股定理,第三条边(斜边)的长为$\sqrt{a^2 + b^2}=\sqrt{3^2 + 4^2}=\sqrt{9 + 16}=\sqrt{25}=5$。
5
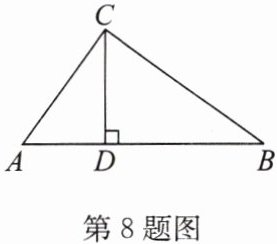
8. 如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$CD是AB$边上的高,若$AC= 6$,$BC= 8$。
(1)求$\triangle ABC的周长l和面积S$;
(2)求$CD$的长。
(1)求$\triangle ABC的周长l和面积S$;
(2)求$CD$的长。

答案:解:
(1)在△ABC中,∠ACB=90°,
∴AB²=AC²+BC²=6²+8²=100,
∴AB=10,
∴l=AB+AC+BC=10+6+8=24,
S= $\frac{1}{2}$AC·BC= $\frac{1}{2}$×6×8=24.
(2)
∵CD是AB边上的高,
∴S_{△ABC}= $\frac{1}{2}$AC·BC= $\frac{1}{2}$AB·CD,
∴CD= $\frac{AC·BC}{AB}$= $\frac{6×8}{10}$=4.8.
(1)在△ABC中,∠ACB=90°,
∴AB²=AC²+BC²=6²+8²=100,
∴AB=10,
∴l=AB+AC+BC=10+6+8=24,
S= $\frac{1}{2}$AC·BC= $\frac{1}{2}$×6×8=24.
(2)
∵CD是AB边上的高,
∴S_{△ABC}= $\frac{1}{2}$AC·BC= $\frac{1}{2}$AB·CD,
∴CD= $\frac{AC·BC}{AB}$= $\frac{6×8}{10}$=4.8.
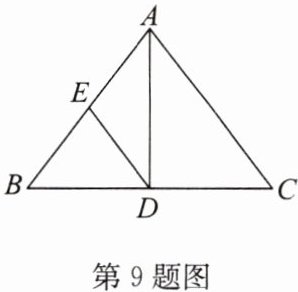
9. 如图,在$\triangle ABC$中,$AB= AC$,$\angle BAC的平分线AD交BC于点D$,$E为AB$的中点。若$BC= 12$,$AD= 8$,求$DE$的长。

答案:解:
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD= $\frac{1}{2}$BC=6.
∵AD=8,
∴在Rt△ABD中,由勾股定理,得AB²=
AD²+BD²=8²+6²=100,
∴AB=10.
又
∵E为Rt△ABD斜边AB的中点,
∴DE= $\frac{1}{2}$AB=5.
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD= $\frac{1}{2}$BC=6.
∵AD=8,
∴在Rt△ABD中,由勾股定理,得AB²=
AD²+BD²=8²+6²=100,
∴AB=10.
又
∵E为Rt△ABD斜边AB的中点,
∴DE= $\frac{1}{2}$AB=5.
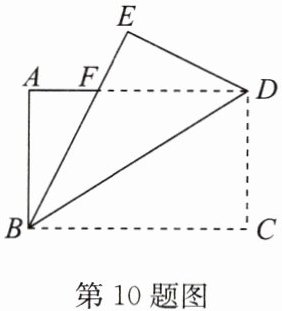
10. 如图,把长方形$ABCD沿对角线BD$折叠,使点$C落在点E$处,$BE交AD于点F$。
(1)求证:点$F在线段BD$的垂直平分线上;
(2)若$BD^{2}= 24$,$DF= 3$,求$AD$的长。
(1)求证:点$F在线段BD$的垂直平分线上;
(2)若$BD^{2}= 24$,$DF= 3$,求$AD$的长。

答案:
(1)证明:
∵△BDE是由△BDC沿直线BD折叠得到的,
∴∠EBD=∠DBC.
∵四边形ABCD是长方形,
∴AD//BC,
∴∠ADB=∠DBC,
∴∠EBD=∠ADB,
∴FB=FD,
∴点F在线段BD的垂直平分线上.
(2)解:设AD=x.
∵DF=3,
∴AF=x-3,BF=3.
在Rt△ABF中,∠A=90°,
∴AB²=BF²-AF².
在Rt△ABD中,∠A=90°,
∴AB²=BD²-AD².
∴BF²-AF²=BD²-AD²,即3²-(x-3)²=24-x²,
∴x=4,
∴AD=4.
(1)证明:
∵△BDE是由△BDC沿直线BD折叠得到的,
∴∠EBD=∠DBC.
∵四边形ABCD是长方形,
∴AD//BC,
∴∠ADB=∠DBC,
∴∠EBD=∠ADB,
∴FB=FD,
∴点F在线段BD的垂直平分线上.
(2)解:设AD=x.
∵DF=3,
∴AF=x-3,BF=3.
在Rt△ABF中,∠A=90°,
∴AB²=BF²-AF².
在Rt△ABD中,∠A=90°,
∴AB²=BD²-AD².
∴BF²-AF²=BD²-AD²,即3²-(x-3)²=24-x²,
∴x=4,
∴AD=4.