1. 基本事实:
三边
分别相等的两个三角形全等,简写成“边边边”或“SSS
”.答案:三边 SSS
2. 符号语言:
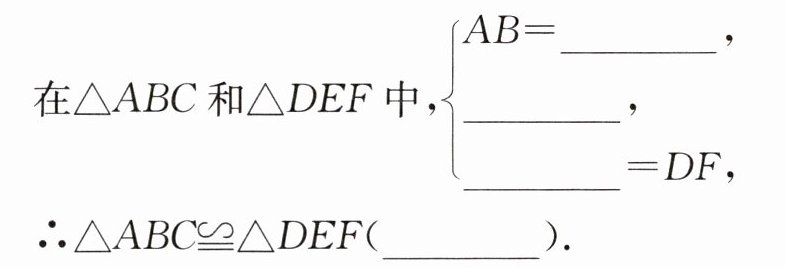
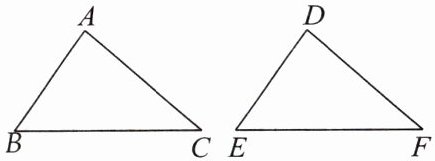


DE
BC=EF
AC
SSS
答案:DE BC=EF AC SSS
3. 三角形
具有
稳定性,四边形不具有
稳定性.答案:具有 不具有
1. 如图,在$\triangle ABC$中,$AB= AC$,$D为BC$的中点. 求证:$AD平分\angle BAC$.
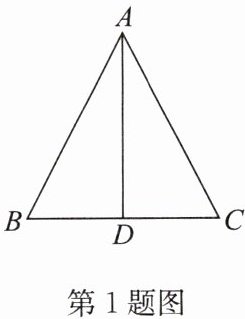

答案:证明:
∵D为BC的中点,
∴BD=CD.
在△ABD和△ACD中,{AB=AC,
BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,即AD平分∠BAC.
∵D为BC的中点,
∴BD=CD.
在△ABD和△ACD中,{AB=AC,
BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,即AD平分∠BAC.
2. 如图,$AB= DC$,$AF= DE$,$BE= CF$. 求证:$\angle A= \angle D$.
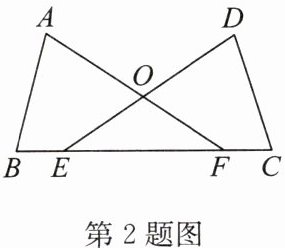

答案:证明:
∵BE=CF,
∴BE+EF=CF+EF,即CE=BF.
在△ABF和△DCE中,{AB=DC,
AF=DE,
BF=CE,
∴△ABF≌△DCE(SSS),
∴∠A=∠D.
∵BE=CF,
∴BE+EF=CF+EF,即CE=BF.
在△ABF和△DCE中,{AB=DC,
AF=DE,
BF=CE,
∴△ABF≌△DCE(SSS),
∴∠A=∠D.
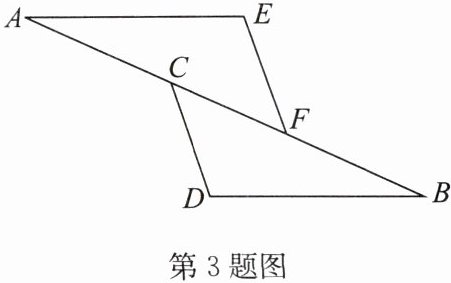
3. 如图,点$A$,$C$,$F$,$B$在同一条直线上,$AC= BF$,$AE= BD$,$EF= CD$. 求证:$\angle AFE= \angle BCD$.

答案:证明:
∵AC=BF,
∴AC+CF=BF+CF,即AF=BC.
在△AEF和△BDC中,{AE=BD,
AF=BC,
EF=DC,
∴△AEF≌△BDC(SSS),
∴∠AFE=∠BCD.
∵AC=BF,
∴AC+CF=BF+CF,即AF=BC.
在△AEF和△BDC中,{AE=BD,
AF=BC,
EF=DC,
∴△AEF≌△BDC(SSS),
∴∠AFE=∠BCD.