1. 判定两个三角形全等的方法有
SAS
、ASA
、AAS
、SSS
.答案:SAS ASA AAS SSS
解析:
SAS、ASA、AAS、SSS
2. 判定两个三角形全等,至少有一个条件是
边相等
.答案:边相等
1. 如图,点A,B,C,D在同一条直线上,且AB= CD,AE= BF,CE= DF.求证:∠E= ∠F.
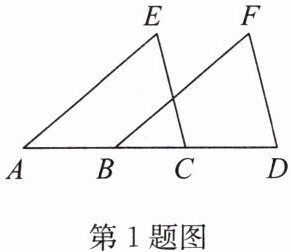

答案:证明:
∵AB=CD,
∴AB+BC=CD+BC,即AC=BD.
又
∵AE=BF,CE=DF,
∴△ACE≌△BDF(SSS),
∴∠E=∠F.
∵AB=CD,
∴AB+BC=CD+BC,即AC=BD.
又
∵AE=BF,CE=DF,
∴△ACE≌△BDF(SSS),
∴∠E=∠F.
2. 如图,点A,B,C,D在同一条直线上,AE//DF,EC//BF,AB= CD.求证:AE= DF.
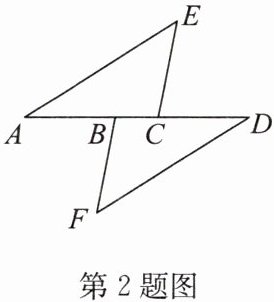

答案:证明:
∵AE//DF,EC//BF,
∴∠A=∠D,∠ACE=∠DBF.
∵AB=CD,
∴AB+BC=CD+BC,即AC=DB.
在△ACE和△DBF中,$\left\{\begin{array}{l} ∠A=∠D,\\ AC=DB,\\ ∠ACE=∠DBF,\end{array}\right. $
∴△ACE≌△DBF(ASA).
∴AE=DF.
∵AE//DF,EC//BF,
∴∠A=∠D,∠ACE=∠DBF.
∵AB=CD,
∴AB+BC=CD+BC,即AC=DB.
在△ACE和△DBF中,$\left\{\begin{array}{l} ∠A=∠D,\\ AC=DB,\\ ∠ACE=∠DBF,\end{array}\right. $
∴△ACE≌△DBF(ASA).
∴AE=DF.
3. 如图,已知AC,BD相交于点O,AD= BC,∠DAO= ∠CBO.求证:△ABD≌△BAC.
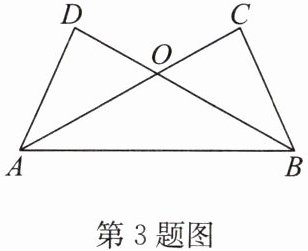

答案:证明:在△ADO和△BCO中,$\left\{\begin{array}{l} ∠DAO=∠CBO,\\ ∠AOD=∠BOC,\\ AD=BC,\end{array}\right. $
∴△ADO≌△BCO(AAS).
∴∠D=∠C,AO=BO,DO=CO.
∴AO+OC=BO+OD,即AC=BD.
又
∵AD=BC,
∴△ABD≌△BAC(SAS).
∴△ADO≌△BCO(AAS).
∴∠D=∠C,AO=BO,DO=CO.
∴AO+OC=BO+OD,即AC=BD.
又
∵AD=BC,
∴△ABD≌△BAC(SAS).