(1) 一个平行四边形的底是 6 厘米,高是 14 厘米,它的面积是(
(2) 一个三角形和一个平行四边形的底和面积分别都相等,三角形的高是 10 厘米,平行四边形的高是(
84
)平方厘米,与它等底等高的三角形的面积是(42
)平方厘米。(2) 一个三角形和一个平行四边形的底和面积分别都相等,三角形的高是 10 厘米,平行四边形的高是(
5
)厘米。答案:84
42
5
42
5
解析:
(1) 平行四边形的面积计算公式是底乘以高,即 $S = a × h$。
代入底 $a = 6$ 厘米和高 $h = 14$ 厘米,得到面积 $S = 6 × 14 = 84$ 平方厘米。
与它等底等高的三角形的面积是平行四边形面积的一半,即 $\frac{1}{2} × 84 = 42$ 平方厘米。
(2) 设三角形的底为 $b$,高为 $h_1 = 10$ 厘米,平行四边形的底也为 $b$,高为 $h_2$。
三角形的面积 $S_1 = \frac{1}{2} × b × h_1 = \frac{1}{2} × b × 10$。
平行四边形的面积 $S_2 = b × h_2$。
因为 $S_1 = S_2$,所以 $\frac{1}{2} × b × 10 = b × h_2$。
解得 $h_2 = 5$ 厘米。
代入底 $a = 6$ 厘米和高 $h = 14$ 厘米,得到面积 $S = 6 × 14 = 84$ 平方厘米。
与它等底等高的三角形的面积是平行四边形面积的一半,即 $\frac{1}{2} × 84 = 42$ 平方厘米。
(2) 设三角形的底为 $b$,高为 $h_1 = 10$ 厘米,平行四边形的底也为 $b$,高为 $h_2$。
三角形的面积 $S_1 = \frac{1}{2} × b × h_1 = \frac{1}{2} × b × 10$。
平行四边形的面积 $S_2 = b × h_2$。
因为 $S_1 = S_2$,所以 $\frac{1}{2} × b × 10 = b × h_2$。
解得 $h_2 = 5$ 厘米。
(1) 两个周长相等的三角形,面积也一定相等。 ………………………………(
(2) 两个等底等高的三角形一定可以拼成一个平行四边形。 …………………(
(3) 三角形的面积等于和它等底等高的平行四边形面积的一半。 ……………(
×
)(2) 两个等底等高的三角形一定可以拼成一个平行四边形。 …………………(
×
)(3) 三角形的面积等于和它等底等高的平行四边形面积的一半。 ……………(
√
)答案:×
×
√
×
√
解析:
(1) 三角形的周长是三条边长度之和,而面积是底与高乘积的一半。周长相等的三角形,其形状和大小可能并不相同,因此面积不一定相等。
(2) 两个等底等高的三角形意味着它们的底和高都相等,但并不意味着它们一定可以拼成一个平行四边形。只有两个完全相同的三角形才能拼成一个平行四边形。
(3) 三角形的面积是底与高乘积的一半,而平行四边形的面积是底与高的乘积。因此,等底等高的三角形的面积确实是等底等高的平行四边形面积的一半。
(2) 两个等底等高的三角形意味着它们的底和高都相等,但并不意味着它们一定可以拼成一个平行四边形。只有两个完全相同的三角形才能拼成一个平行四边形。
(3) 三角形的面积是底与高乘积的一半,而平行四边形的面积是底与高的乘积。因此,等底等高的三角形的面积确实是等底等高的平行四边形面积的一半。
3. 求下图中阴影三角形的面积。(单位:厘米)
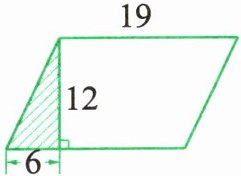



答案:12×6÷2=36(平方厘米)
12×7÷2=42(平方厘米)
12×7÷2=42(平方厘米)
我很棒 4. 下图是一些等边三角形,要把一个等边三角形的面积平均分成 2 份,可以怎样分?如果平均分成 3 份呢?画画看。(提示:有不同的画法)


答案:


5. 准备一张边长为 4 厘米的正方形纸,从一边的中点到邻边的中点画一条线段,沿着这条线段剪去一个角,你知道剩下部分的面积是多少吗?剪一剪,算一算。


答案:4÷2=2(厘米)
4×4-2×2÷2=14 (平方厘米)
答:剩下部分的面积是14平方厘米。
4×4-2×2÷2=14 (平方厘米)
答:剩下部分的面积是14平方厘米。