活动一:想一想 说一说
一元二次方程$x^{2}-2x - 3 = 0$与二次函数$y = x^{2}-2x - 3$有哪些联系?
一元二次方程$x^{2}-2x - 3 = 0$与二次函数$y = x^{2}-2x - 3$有哪些联系?
答案:解:二次函数y=x²-2x-3与x轴的交点的横坐标就是一元二次方程x²-2x-3=0的根
活动二:做一做 比一比
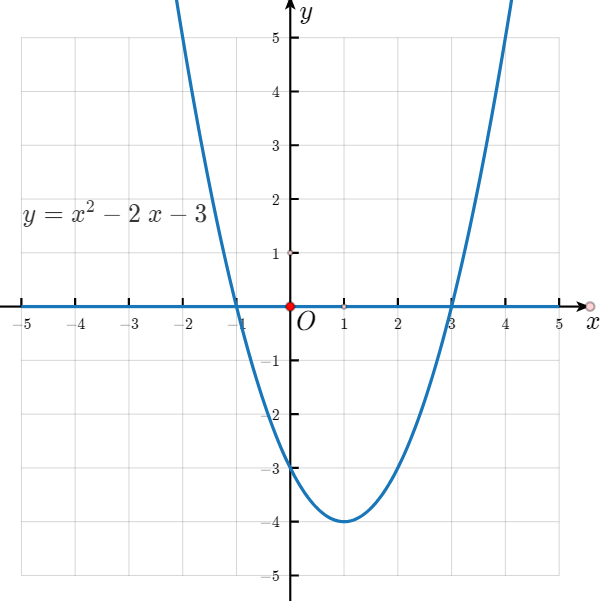
请你在图 5 - 6 中画出二次函数$y = x^{2}-2x - 3$的图像.图像上是否有一些特殊的点与一元二次方程$x^{2}-2x - 3 = 0$的根之间有某种联系?你有什么发现?

请你在图 5 - 6 中画出二次函数$y = x^{2}-2x - 3$的图像.图像上是否有一些特殊的点与一元二次方程$x^{2}-2x - 3 = 0$的根之间有某种联系?你有什么发现?

答案:
解:图像与x轴交点的横坐标
是该一元二次方程的根
解:图像与x轴交点的横坐标
是该一元二次方程的根

活动三:看一看 议一议
1. 观察课本图 5 - 10,直接说出方程$-\frac{1}{2}x^{2}-4x - 6 = 0$、$x^{2}-6x + 9 = 0$和$x^{2}-2x + 3 = 0$的解的情况.写出函数$y = -\frac{1}{2}x^{2}-4x - 6$、$y = x^{2}-6x + 9$、$y = x^{2}-2x + 3$的图像与$x$轴的公共点的坐标,它们与$x$轴的公共点有几个?它们与方程的根有何关系?
2. 二次函数$y = ax^{2}+bx + c$的图像与一元二次方程$ax^{2}+bx + c = 0$的根有何关系?你能由一元二次方程$ax^{2}+bx + c = 0$的根的情况说出二次函数$y = ax^{2}+bx + c$的图像与$x$轴的位置关系吗?
1. 观察课本图 5 - 10,直接说出方程$-\frac{1}{2}x^{2}-4x - 6 = 0$、$x^{2}-6x + 9 = 0$和$x^{2}-2x + 3 = 0$的解的情况.写出函数$y = -\frac{1}{2}x^{2}-4x - 6$、$y = x^{2}-6x + 9$、$y = x^{2}-2x + 3$的图像与$x$轴的公共点的坐标,它们与$x$轴的公共点有几个?它们与方程的根有何关系?
2. 二次函数$y = ax^{2}+bx + c$的图像与一元二次方程$ax^{2}+bx + c = 0$的根有何关系?你能由一元二次方程$ax^{2}+bx + c = 0$的根的情况说出二次函数$y = ax^{2}+bx + c$的图像与$x$轴的位置关系吗?
答案:解:$-\frac {1}{2}x²-4x- 6= 0$的解为$x_{1}= -6,$$ x_{2}= -2$
x²-6x+9=0的解为$x_{1} =x_{2}= 3$
x²-2x+3=0无解
$y=-\frac {1}{2}x²- 4x- 6$与x轴的公共点为(-6, 0)、 (-2, 0)
y=x²-6x+9与x轴的公共点为(3 , 0)
y=x²-2x+3与x轴无公共点
二次函数与x轴有公共点,则公共点的横坐标就是方程的根;
二次函数与x轴无公共点,则方程无解。
解:一般地,二次函数y= ax²+bx+c 的图像与一元二次方程ax²+bx+c=0的根有如下关系:
如果二次函数y= ax²+ bx+ c 的图像与x轴有两个公共点,
那么一元二次方程ax²+ bx+c= 0有两个不相等的实数根;
如果二次函数y= ax²+bx+c 的图像与x轴有且只有一个公共点,
那么一元二次方程ax²+ bx+ c= 0有两个相等的实数根;
如果二次函数y= ax²+ bx + c 的图像与x轴没有公共点,
那么一元二次方程ax²+ bx+c= 0没有实数根
反过来,由一元二次方程ax²+ bx + c = 0的根的情况,
可以知道二次函数y= ax²+ bx + c 的图像与x轴的位置关系。
x²-6x+9=0的解为$x_{1} =x_{2}= 3$
x²-2x+3=0无解
$y=-\frac {1}{2}x²- 4x- 6$与x轴的公共点为(-6, 0)、 (-2, 0)
y=x²-6x+9与x轴的公共点为(3 , 0)
y=x²-2x+3与x轴无公共点
二次函数与x轴有公共点,则公共点的横坐标就是方程的根;
二次函数与x轴无公共点,则方程无解。
解:一般地,二次函数y= ax²+bx+c 的图像与一元二次方程ax²+bx+c=0的根有如下关系:
如果二次函数y= ax²+ bx+ c 的图像与x轴有两个公共点,
那么一元二次方程ax²+ bx+c= 0有两个不相等的实数根;
如果二次函数y= ax²+bx+c 的图像与x轴有且只有一个公共点,
那么一元二次方程ax²+ bx+ c= 0有两个相等的实数根;
如果二次函数y= ax²+ bx + c 的图像与x轴没有公共点,
那么一元二次方程ax²+ bx+c= 0没有实数根
反过来,由一元二次方程ax²+ bx + c = 0的根的情况,
可以知道二次函数y= ax²+ bx + c 的图像与x轴的位置关系。