1. 如图,$l_1// l_2// l_3$,那么$\frac{AB}{BD}=$
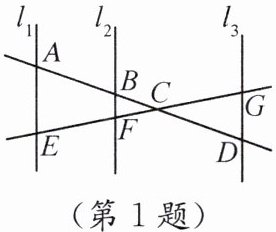
$\frac{EF}{FG}$
,$\frac{EG}{FG}=$$\frac{AD}{BD}$
.
答案:$ \frac {EF}{FG}$
$ \frac {AD}{BD}$
$ \frac {AD}{BD}$
2. 如图,在$\triangle ABC$中,$DE// BC$.
(1) 若$AD = 3$,$AB = 9$,$DE = 4$,则$BC =$
(2) 若$DE:BC = 2:5$,则$AD:DB =$
(3) 若$BC = 7$,$DE = 4$,$AE = 8$,则$EC =$
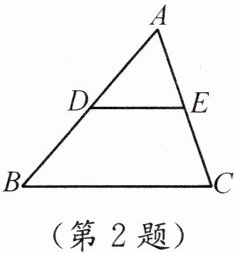
(1) 若$AD = 3$,$AB = 9$,$DE = 4$,则$BC =$
12
;(2) 若$DE:BC = 2:5$,则$AD:DB =$
2:3
;(3) 若$BC = 7$,$DE = 4$,$AE = 8$,则$EC =$
6
.
答案:12
2:3
6
2:3
6
3. 已知:如图,$EG// BC$,$GF// CD$.
求证:$\frac{AE}{AB}=\frac{AF}{AD}$.
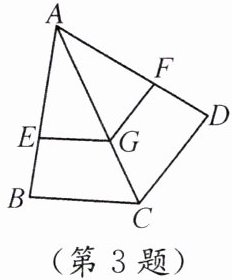
求证:$\frac{AE}{AB}=\frac{AF}{AD}$.

答案:6
证明:∵EG//BC
∴$\frac {AE}{AB}=\frac {AG}{AC}$
∵GF//CD
∴$\frac {AF}{AD}=\frac {AG}{AC}$
∴$\frac {AE}{AB}=\frac {AF}{AD}$
证明:∵EG//BC
∴$\frac {AE}{AB}=\frac {AG}{AC}$
∵GF//CD
∴$\frac {AF}{AD}=\frac {AG}{AC}$
∴$\frac {AE}{AB}=\frac {AF}{AD}$
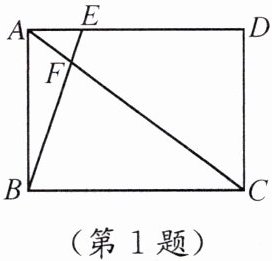
1. 如图,在矩形$ABCD$中,若$AB = 3$,$AC = 5$,$\frac{AF}{FC}=\frac{1}{4}$,则$AE$的长为
1
.
答案:1. 首先,根据矩形的性质求$BC$的长度:
在矩形$ABCD$中,$\angle ABC = 90^{\circ}$,已知$AB = 3$,$AC = 5$,根据勾股定理$BC=\sqrt{AC^{2}-AB^{2}}$。
由勾股定理$a^{2}+b^{2}=c^{2}$(这里$c = AC$,$a = AB$,$b = BC$),则$BC=\sqrt{5^{2}-3^{2}}=\sqrt{25 - 9}=\sqrt{16}=4$。
因为$AD// BC$,所以$\triangle AEF\sim\triangle CBF$。
2. 然后,根据相似三角形的性质:
对于相似三角形$\triangle AEF$和$\triangle CBF$,由相似三角形对应边成比例,可得$\frac{AE}{BC}=\frac{AF}{FC}$。
已知$\frac{AF}{FC}=\frac{1}{4}$,$BC = 4$。
设$AE=x$,根据$\frac{AE}{BC}=\frac{AF}{FC}$,即$\frac{x}{4}=\frac{1}{4}$。
所以$AE = 1$。
在矩形$ABCD$中,$\angle ABC = 90^{\circ}$,已知$AB = 3$,$AC = 5$,根据勾股定理$BC=\sqrt{AC^{2}-AB^{2}}$。
由勾股定理$a^{2}+b^{2}=c^{2}$(这里$c = AC$,$a = AB$,$b = BC$),则$BC=\sqrt{5^{2}-3^{2}}=\sqrt{25 - 9}=\sqrt{16}=4$。
因为$AD// BC$,所以$\triangle AEF\sim\triangle CBF$。
2. 然后,根据相似三角形的性质:
对于相似三角形$\triangle AEF$和$\triangle CBF$,由相似三角形对应边成比例,可得$\frac{AE}{BC}=\frac{AF}{FC}$。
已知$\frac{AF}{FC}=\frac{1}{4}$,$BC = 4$。
设$AE=x$,根据$\frac{AE}{BC}=\frac{AF}{FC}$,即$\frac{x}{4}=\frac{1}{4}$。
所以$AE = 1$。
2. 如图,在$\triangle ABC$中,$D$是边$BC$的中点,$E$是边$AC$上的任意一点,$BE$交$AD$于点$O$.
(1) 当$\frac{AE}{AC}=\frac{1}{2}$时,求$\frac{AO}{AD}$的值;
(2) 当$\frac{AE}{AC}=\frac{1}{3}$时,求$\frac{AO}{AD}$的值;
(3) 当$\frac{AE}{AC}=\frac{1}{4}$时,求$\frac{AO}{AD}$的值;
(4) 当$\frac{AE}{AC}=\frac{1}{n + 1}$时,试猜想$\frac{AO}{AD}$的值,并证明你的猜想.

(1) 当$\frac{AE}{AC}=\frac{1}{2}$时,求$\frac{AO}{AD}$的值;
(2) 当$\frac{AE}{AC}=\frac{1}{3}$时,求$\frac{AO}{AD}$的值;
(3) 当$\frac{AE}{AC}=\frac{1}{4}$时,求$\frac{AO}{AD}$的值;
(4) 当$\frac{AE}{AC}=\frac{1}{n + 1}$时,试猜想$\frac{AO}{AD}$的值,并证明你的猜想.

答案:解:过点D作DF//BE,交AC于点F
∵DF//BE
∴$\frac {CF}{CE}=\frac {CD}{BC}=\frac {1}{2}$
∴点F 为CE的中点
∵DF//BE
∴$\frac {AO}{AD}=\frac {AE}{AF}$
(1)∵$\frac {AE}{AC}=\frac {1}{2}$
∴$\frac {AE}{AF}=\frac {2}{3}$
∴$\frac {AO}{AD}=\frac {2}{3}$
(2)∵$\frac {AE}{AC}=\frac {1}{3}$
∴$\frac {AE}{AF}=\frac {1}{2}$
∴$\frac {AO}{AD}=\frac {1}{2}$
(3)∵$\frac {AE}{AC}=\frac {1}{4}$
∴$\frac {AE}{AF}=\frac {2}{5}$
∴$\frac {AO}{AD}=\frac {2}{5}$
(4)∵$\frac {AE}{AC}=\frac {1}{n+1}$
∴$\frac {AE}{AF}=\frac {2}{n+2}$
∴$\frac {AO}{AD}=\frac {2}{n+2}$
∵DF//BE
∴$\frac {CF}{CE}=\frac {CD}{BC}=\frac {1}{2}$
∴点F 为CE的中点
∵DF//BE
∴$\frac {AO}{AD}=\frac {AE}{AF}$
(1)∵$\frac {AE}{AC}=\frac {1}{2}$
∴$\frac {AE}{AF}=\frac {2}{3}$
∴$\frac {AO}{AD}=\frac {2}{3}$
(2)∵$\frac {AE}{AC}=\frac {1}{3}$
∴$\frac {AE}{AF}=\frac {1}{2}$
∴$\frac {AO}{AD}=\frac {1}{2}$
(3)∵$\frac {AE}{AC}=\frac {1}{4}$
∴$\frac {AE}{AF}=\frac {2}{5}$
∴$\frac {AO}{AD}=\frac {2}{5}$
(4)∵$\frac {AE}{AC}=\frac {1}{n+1}$
∴$\frac {AE}{AF}=\frac {2}{n+2}$
∴$\frac {AO}{AD}=\frac {2}{n+2}$