活动:画一画 想一想
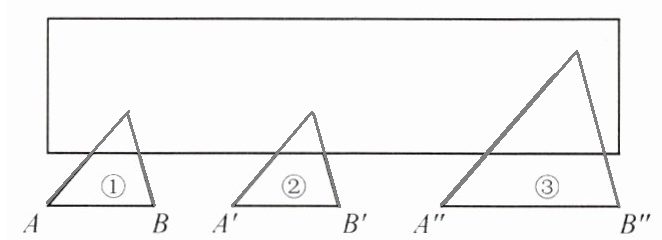
(1) 如图 6-5,小明用白纸遮住了 3 个三角形的一部分,你能画出这 3 个三角形吗?如果能,请补全这 3 个三角形.

(2) 在图 6-5 中,如果$\angle A = \angle A'$,$\angle B = \angle B'$,$AB = A'B'$,那么三角形①与三角形②全等吗?如果$\angle A'' = \angle A$,$\angle B'' = \angle B$,请你猜想三角形①与三角形③是否相似.
(3) 小林为了验证三角形①与三角形③是否相似,将三角形①平移,使点$A$与点$A''$重合,$AB$落在$A''B''$上,$AC$落在$A''C''$上(图 6-6).他认为这样操作可以证明$\triangle ABC \sim \triangle A''B''C''$,为什么?

(4) 上面的操作说明了什么?把你的发现与同学交流.
(1) 如图 6-5,小明用白纸遮住了 3 个三角形的一部分,你能画出这 3 个三角形吗?如果能,请补全这 3 个三角形.

(2) 在图 6-5 中,如果$\angle A = \angle A'$,$\angle B = \angle B'$,$AB = A'B'$,那么三角形①与三角形②全等吗?如果$\angle A'' = \angle A$,$\angle B'' = \angle B$,请你猜想三角形①与三角形③是否相似.
(3) 小林为了验证三角形①与三角形③是否相似,将三角形①平移,使点$A$与点$A''$重合,$AB$落在$A''B''$上,$AC$落在$A''C''$上(图 6-6).他认为这样操作可以证明$\triangle ABC \sim \triangle A''B''C''$,为什么?

(4) 上面的操作说明了什么?把你的发现与同学交流.
答案:
解:三角形①和三角形②全等,三角形①和三角形③相似
在△ABC和△A'B'C'中
$\begin{cases}{∠A=∠A' }\\{AB=A'B'} \\{∠B=∠B'} \end{cases}$
∴$△ABC≌△A'B'C'(\mathrm {ASA})$
解:∵∠A=∠A'',∴AC落在A''C''上
∵∠B=∠B',∴BC//B''C''
∴△ABC∽△A''B''C''
解:如果一个三角形的两个角与另一个三角形的两个角对应相等,
那么这两个三角形相似。
解:三角形①和三角形②全等,三角形①和三角形③相似
在△ABC和△A'B'C'中
$\begin{cases}{∠A=∠A' }\\{AB=A'B'} \\{∠B=∠B'} \end{cases}$
∴$△ABC≌△A'B'C'(\mathrm {ASA})$
解:∵∠A=∠A'',∴AC落在A''C''上
∵∠B=∠B',∴BC//B''C''
∴△ABC∽△A''B''C''
解:如果一个三角形的两个角与另一个三角形的两个角对应相等,
那么这两个三角形相似。

1. 下列说法中,不正确的是(
A.有一个底角对应相等的两个等腰三角形相似
B.有一个角对应相等的两个等腰三角形相似
C.所有等边三角形都相似
D.顶角对应相等的两个等腰三角形相似
B
).A.有一个底角对应相等的两个等腰三角形相似
B.有一个角对应相等的两个等腰三角形相似
C.所有等边三角形都相似
D.顶角对应相等的两个等腰三角形相似
答案:B