活动一:做一做 证一证
如图6-9,已知$\triangle ABC$.
(1) 作$\triangle A^{\prime}B^{\prime}C^{\prime}$,使得$\frac{AB}{A^{\prime}B^{\prime}} = \frac{AC}{A^{\prime}C^{\prime}} = \frac{BC}{B^{\prime}C^{\prime}} = 2$;
(2) 比较$\angle A$与$\angle A^{\prime}$的大小,由此你能判断$\triangle ABC$与$\triangle A^{\prime}B^{\prime}C^{\prime}$相似吗?为什么?
(3) 设$\frac{AB}{A^{\prime}B^{\prime}} = \frac{AC}{A^{\prime}C^{\prime}} = \frac{BC}{B^{\prime}C^{\prime}} = k$,改变$k$的值再试一试,$\triangle ABC$与$\triangle A^{\prime}B^{\prime}C^{\prime}$是否相似?证明你的判断.

如图6-9,已知$\triangle ABC$.
(1) 作$\triangle A^{\prime}B^{\prime}C^{\prime}$,使得$\frac{AB}{A^{\prime}B^{\prime}} = \frac{AC}{A^{\prime}C^{\prime}} = \frac{BC}{B^{\prime}C^{\prime}} = 2$;
(2) 比较$\angle A$与$\angle A^{\prime}$的大小,由此你能判断$\triangle ABC$与$\triangle A^{\prime}B^{\prime}C^{\prime}$相似吗?为什么?
(3) 设$\frac{AB}{A^{\prime}B^{\prime}} = \frac{AC}{A^{\prime}C^{\prime}} = \frac{BC}{B^{\prime}C^{\prime}} = k$,改变$k$的值再试一试,$\triangle ABC$与$\triangle A^{\prime}B^{\prime}C^{\prime}$是否相似?证明你的判断.

答案:
解:(1)如图所示
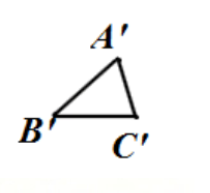
(2)∠A=∠A,△ABC∽△A'B'C'
在AB上截取AB''= A'B',过点B''作B''C''//BC,交AC于点C''
在△ABC和△AB''C''中
∵B''C''//BC
∴$△ABC \sim △AB''C''$
∴$\frac {AB}{AB''}=\frac {BC}{B''C''}=\frac {CA}{C''A}$
∵$\frac {AB}{A'B'}=\frac {BC}{B'C'}=\frac {CA}{C'A'},$AB''= A'B'
∴B''C''= B'C',C''A= C'A',△AB''C''≌△A'B'C'
∴$△ABC \sim △A'B'C'$
(3)假设AB>A'B',在AB上截取AB''= A'B',过点B''作B''C''//BC,交AC于点C''
在△ABC和△AB''C''中
∵B''C''//BC
∴$△ABC \sim △AB''C''$
∴$\frac {AB}{AB''}=\frac {BC}{B''C''}=\frac {CA}{C''A}$
∵$\frac {AB}{A'B'}=\frac {BC}{B'C'}=\frac {CA}{C'A'},$AB''= A'B'
∴B''C''= B'C',C''A= C'A',△AB''C''≌△A'B'C'
∴$△ABC \sim △A'B'C'$
解:(1)如图所示
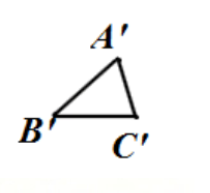
(2)∠A=∠A,△ABC∽△A'B'C'
在AB上截取AB''= A'B',过点B''作B''C''//BC,交AC于点C''
在△ABC和△AB''C''中
∵B''C''//BC
∴$△ABC \sim △AB''C''$
∴$\frac {AB}{AB''}=\frac {BC}{B''C''}=\frac {CA}{C''A}$
∵$\frac {AB}{A'B'}=\frac {BC}{B'C'}=\frac {CA}{C'A'},$AB''= A'B'
∴B''C''= B'C',C''A= C'A',△AB''C''≌△A'B'C'
∴$△ABC \sim △A'B'C'$
(3)假设AB>A'B',在AB上截取AB''= A'B',过点B''作B''C''//BC,交AC于点C''
在△ABC和△AB''C''中
∵B''C''//BC
∴$△ABC \sim △AB''C''$
∴$\frac {AB}{AB''}=\frac {BC}{B''C''}=\frac {CA}{C''A}$
∵$\frac {AB}{A'B'}=\frac {BC}{B'C'}=\frac {CA}{C'A'},$AB''= A'B'
∴B''C''= B'C',C''A= C'A',△AB''C''≌△A'B'C'
∴$△ABC \sim △A'B'C'$
活动二:想一想 说一说
通过上面的探索,归纳所发现的判定三角形相似的条件.
通过上面的探索,归纳所发现的判定三角形相似的条件.
答案:解:三边成比例的两个三角形相似
1. 在$\triangle ABC$和$\triangle A^{\prime}B^{\prime}C^{\prime}$中,有下列条件:①$\frac{AB}{A^{\prime}B^{\prime}} = \frac{BC}{B^{\prime}C^{\prime}}$;②$\frac{AC}{A^{\prime}C^{\prime}} = \frac{BC}{B^{\prime}C^{\prime}}$;③$\angle A = \angle A^{\prime}$;
④$\angle C = \angle C^{\prime}$.从中任选两个条件,能判定$\triangle ABC \sim \triangle A^{\prime}B^{\prime}C^{\prime}$的选法有(
A.1种
B.2种
C.3种
D.4种
④$\angle C = \angle C^{\prime}$.从中任选两个条件,能判定$\triangle ABC \sim \triangle A^{\prime}B^{\prime}C^{\prime}$的选法有(
C
).A.1种
B.2种
C.3种
D.4种
答案:C
2. 在$\triangle ABC$和$\triangle DEF$中,$AB = 4$,$BC = 5$,$AC = 8$,$DE = 6$,$DF = 12$.当$EF =$
7.5
时,$\triangle ABC \sim \triangle DEF$.答案:7.5
3. 等腰三角形$ABC$的腰长为$18 cm$,底边长为$6 cm$,在腰$AC$上取一点$D$,使$\triangle ABC \sim \triangle BDC$,则$DC =$
2
$ cm$.答案:2
4. 一个铝制三角形框架的三条边长分别为$24 cm$、$30 cm$、$36 cm$,再做一个与它相似的铝制三角形框架,现有长分别为$27 cm$、$45 cm$的两根铝材,要求以其中的一根为一边,另一根截下两段(允许有余料)作为另外两边,截法有(
A.0种
B.1种
C.2种
D.3种
B
).A.0种
B.1种
C.2种
D.3种
答案:B