5. 如图,在$\triangle ABC$中,$AB = 6$,$AC = 4$,$P$是$AC$的中点,过点$P$的直线交$AB$于点$Q$,若以$A$、
$P$、$Q$为顶点的三角形与以$A$、$B$、$C$为顶点的三角形相似,求$AQ$的长.

$P$、$Q$为顶点的三角形与以$A$、$B$、$C$为顶点的三角形相似,求$AQ$的长.

答案:解:若△AQP∽△ABC
则有$\frac {AQ}{AB}=\frac {AP}{AC},$即$\frac {AQ}6=\frac 12$
∴AQ=3
若△APQ∽△ABC
则有$\frac {AP}{AB}=\frac {AQ}{AC},$即$\frac {2}6=\frac {AQ}4$
∴$AQ=\frac {4}{3}$
综上,AQ 的长为3或$\frac 43$
则有$\frac {AQ}{AB}=\frac {AP}{AC},$即$\frac {AQ}6=\frac 12$
∴AQ=3
若△APQ∽△ABC
则有$\frac {AP}{AB}=\frac {AQ}{AC},$即$\frac {2}6=\frac {AQ}4$
∴$AQ=\frac {4}{3}$
综上,AQ 的长为3或$\frac 43$
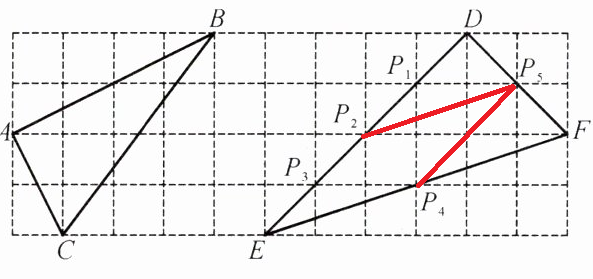
1. 如图,方格纸中每个小正方形的边长都为$1$,$\triangle ABC$与$\triangle DEF$的顶点都在格点上.
(1) 判断$\triangle ABC$与$\triangle DEF$是否相似,并说明理由.
(2)$P_1$、$P_2$、$P_3$、$P_4$、$P_5$、$D$、$F$是$\triangle DEF$边上的$7$个格点,请在这$7$个格点中选取$3$个作为三角形的顶点,使构成的三角形与$\triangle ABC$相似(要求写出$2$个符合条件的三角形,并在图中连接相应线段,不必说明理由).

(1) 判断$\triangle ABC$与$\triangle DEF$是否相似,并说明理由.
(2)$P_1$、$P_2$、$P_3$、$P_4$、$P_5$、$D$、$F$是$\triangle DEF$边上的$7$个格点,请在这$7$个格点中选取$3$个作为三角形的顶点,使构成的三角形与$\triangle ABC$相似(要求写出$2$个符合条件的三角形,并在图中连接相应线段,不必说明理由).

答案:
解: (1)相似
$AB=2\sqrt{5},$$AC=\sqrt{5},$BC=5
$DE= 4\sqrt{2},$$DF= 2\sqrt{2},$$EF= 2\sqrt{10}$
∴$\frac {AC}{DF}=\frac {AB}{DE}=\frac {BC}{EF}=\frac {\sqrt{10}}{4} $
∴△ABC∽△DEF
$(2)△{P}_2{P}_5D,$${P}_4{P}_5F$
解: (1)相似
$AB=2\sqrt{5},$$AC=\sqrt{5},$BC=5
$DE= 4\sqrt{2},$$DF= 2\sqrt{2},$$EF= 2\sqrt{10}$
∴$\frac {AC}{DF}=\frac {AB}{DE}=\frac {BC}{EF}=\frac {\sqrt{10}}{4} $
∴△ABC∽△DEF
$(2)△{P}_2{P}_5D,$${P}_4{P}_5F$

2. 学习本章后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件.
(1) “对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形全等”.类似地,可以得到:满足
(2) “满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,可以得到:满足

已知:如图,
求证:$ Rt \triangle ABC \sim Rt \triangle A^{\prime}B^{\prime}C^{\prime}$.
(1) “对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形全等”.类似地,可以得到:满足
一个锐角对应相等
或两直角边对应成比例
,两个直角三角形相似.(2) “满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,可以得到:满足
斜边和一条直角边对应成比例
的两个直角三角形相似.请你结合右图,写出已知,并完成说理过程.
已知:如图,
在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,$\frac{AB}{A'B'}=\frac{BC}{B'C'}$.
求证:$ Rt \triangle ABC \sim Rt \triangle A^{\prime}B^{\prime}C^{\prime}$.
答案:一个锐角对应相等
两直角边对应成比例
斜边和一条直角边对应成比例
在Rt△ABC和Rt△A'B'C',∠C=∠C'=90°,$\frac {AB}{A'B'}=\frac {BC}{B'C'}$
证明:设$\frac {AB}{A'B'}=\frac {BC}{B'C'}=k$
则AB=kA'B',BC=kB'C'
∵∠C=∠C'=90°
∴AC²= AB²- BC²,A'C'²= A'B'²- B'C'²
∴AC²=k²(A'B'²-B'C'²)= k²A'C'²
∴AC= kA'C'
∴$\frac {AB}{A'B'}=\frac {AC}{A'C'}=\frac {BC}{B'C'}$
∴Rt△ABC∽Rt△A'B'C'
两直角边对应成比例
斜边和一条直角边对应成比例
在Rt△ABC和Rt△A'B'C',∠C=∠C'=90°,$\frac {AB}{A'B'}=\frac {BC}{B'C'}$
证明:设$\frac {AB}{A'B'}=\frac {BC}{B'C'}=k$
则AB=kA'B',BC=kB'C'
∵∠C=∠C'=90°
∴AC²= AB²- BC²,A'C'²= A'B'²- B'C'²
∴AC²=k²(A'B'²-B'C'²)= k²A'C'²
∴AC= kA'C'
∴$\frac {AB}{A'B'}=\frac {AC}{A'C'}=\frac {BC}{B'C'}$
∴Rt△ABC∽Rt△A'B'C'