2. 如图,在$\triangle ABC$中,三条中线交于点$G$,$BG:FG =$

2:1
,$S_{\triangle ABG}:S_{\triangle ABC}=$1:3
.
答案:2:1
1:3
1:3
3. 如图,$\triangle ADE$和$\triangle ABC$有一个公共顶点$A$,$\angle1 = \angle2$.
(1) 请你添加一个适当的条件,使$\triangle ADE∽\triangle ABC$:
(2) 由(1),你能否得到其他的相似三角形?如果能,请说明理由.

(1) 请你添加一个适当的条件,使$\triangle ADE∽\triangle ABC$:
∠ADE=∠ABC等
.(2) 由(1),你能否得到其他的相似三角形?如果能,请说明理由.

答案:∠ADE=∠ABC
解: (2)能。△ADB∽△AEC
∵△ADE∽△ABC
∴$\frac {AD}{AE}=\frac {AB}{AC}$
∵∠1=∠2
∴△ADB∽△AEC
解: (2)能。△ADB∽△AEC
∵△ADE∽△ABC
∴$\frac {AD}{AE}=\frac {AB}{AC}$
∵∠1=∠2
∴△ADB∽△AEC
4. 如图,$\triangle ABC$的中线$AE$、$BD$相交于点$G$,$DF// BC$,交$AE$于点$F$.求$\frac{FG}{AE}$的值.

答案:解:∵DF//BC
∴$\frac {FG}{GE}=\frac {DF}{BE}=\frac {1}{2}$
∵点G 是△ABC的重心
∴$\frac {GE}{AE}=\frac {1}{3}$
∴$\frac {FG}{AE}=\frac {1}{6}$
∴$\frac {FG}{GE}=\frac {DF}{BE}=\frac {1}{2}$
∵点G 是△ABC的重心
∴$\frac {GE}{AE}=\frac {1}{3}$
∴$\frac {FG}{AE}=\frac {1}{6}$
1. 将三角形纸片$ABC$按如图所示的方式折叠,使点$B$落在边$AC$上,记为点$B'$,折痕为$EF$.已知$AB = AC = 3$,$BC = 4$,如果以$B'$、$F$、$C$为顶点的三角形与$\triangle ABC$相似,那么$BF$的长是
$\frac{12}{7}$或2
.
答案:$\frac {12}{7}$或2
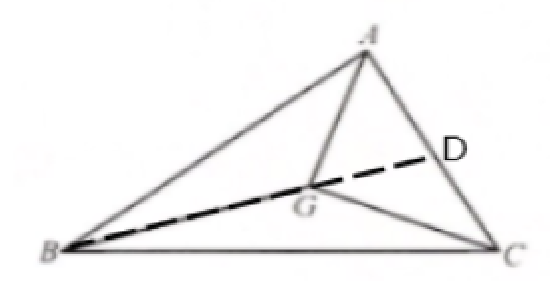
2. 如图,点$G$是$\triangle ABC$的重心,$AG\perp GC$,$AG = 3$,$GC = 4$.求$BG$的长.

答案:
解:延长BG 交AC于点D
则点D是AC的中点
∴在Rt△ACG 中,$DG=\frac {1}{2}AC =\frac {5}{2}$
∴BG=2DG= 5
解:延长BG 交AC于点D
则点D是AC的中点
∴在Rt△ACG 中,$DG=\frac {1}{2}AC =\frac {5}{2}$
∴BG=2DG= 5
