活动一:想一想 试一试
1. 根据相似三角形和相似多边形的定义,能得到什么性质?
2. 马路旁边原有一个周长为 80 m 的三角形绿地 ABC(图 6 - 12),由于马路拓宽,绿地被“削”去一个角,变成了四边形绿地 BCED,其中 BC//DE,已知原绿地的一边 AB 的长由 30 m 缩短成 18 m,那么被“削”去部分的周长是多少?

3. 两个相似多边形周长之间有什么关系?说明你的理由.
1. 根据相似三角形和相似多边形的定义,能得到什么性质?
2. 马路旁边原有一个周长为 80 m 的三角形绿地 ABC(图 6 - 12),由于马路拓宽,绿地被“削”去一个角,变成了四边形绿地 BCED,其中 BC//DE,已知原绿地的一边 AB 的长由 30 m 缩短成 18 m,那么被“削”去部分的周长是多少?

3. 两个相似多边形周长之间有什么关系?说明你的理由.
答案:解:相似三角形和相似多边形对应边成比例,对应角相等
解:∵BC//DE
∴△ADE∽△ABC
∵$\frac {AD}{AB}=\frac {12}{30}=\frac {2}{5}$
∴削去部分的周长是$\frac {2}{5}×80=32m$
解:相似多边形周长之比等于相似比。
解:∵BC//DE
∴△ADE∽△ABC
∵$\frac {AD}{AB}=\frac {12}{30}=\frac {2}{5}$
∴削去部分的周长是$\frac {2}{5}×80=32m$
解:相似多边形周长之比等于相似比。
活动二:议一议 证一证
1. 如图 6 - 13,△ABC∽△A′B′C′,相似比为 k,AD 与 A′D′分别是△ABC 和△A′B′C′的边 BC、B′C′上的高. 试说明$\frac{AD}{A'D'}=k$.
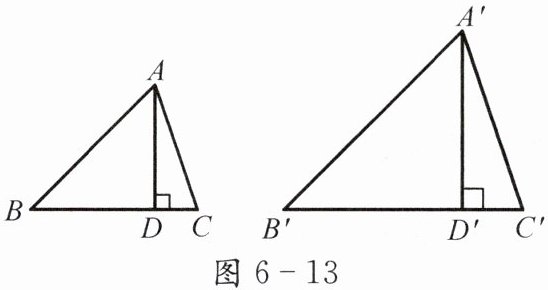
2. 你能猜想并证明相似三角形对应高之间的关系吗?
3. 两个相似三角形的面积之间有怎样的关系?为什么?两个相似多边形的面积之间又有怎样的关系?
1. 如图 6 - 13,△ABC∽△A′B′C′,相似比为 k,AD 与 A′D′分别是△ABC 和△A′B′C′的边 BC、B′C′上的高. 试说明$\frac{AD}{A'D'}=k$.

2. 你能猜想并证明相似三角形对应高之间的关系吗?
3. 两个相似三角形的面积之间有怎样的关系?为什么?两个相似多边形的面积之间又有怎样的关系?
答案:解:∵△ABC∽△A'B'C'
∴∠B=∠B'
∵AD与A'D'分别是△ABC和△A'B'C'中边BC、 B'C'上的高
∴∠ADB=∠A'D'B'=90°
∴△ABD∽△A'B'D'
∴$\frac {AB}{A'B'}=\frac {AD}{A'D'}=k$
解:相似三角形对应高之比等于相似比。
解:相似三角形的面积之比等于相似比的平方。
相似多边形的面积之比等于相似比的平方。
∴∠B=∠B'
∵AD与A'D'分别是△ABC和△A'B'C'中边BC、 B'C'上的高
∴∠ADB=∠A'D'B'=90°
∴△ABD∽△A'B'D'
∴$\frac {AB}{A'B'}=\frac {AD}{A'D'}=k$
解:相似三角形对应高之比等于相似比。
解:相似三角形的面积之比等于相似比的平方。
相似多边形的面积之比等于相似比的平方。
1. 已知△ADE 与△ABC 的相似比为$1:2$,则△ADE 与△ABC 的面积比为(
A.$1:2$
B.$1:4$
C.$2:1$
D.$4:1$
B
).A.$1:2$
B.$1:4$
C.$2:1$
D.$4:1$
答案:B