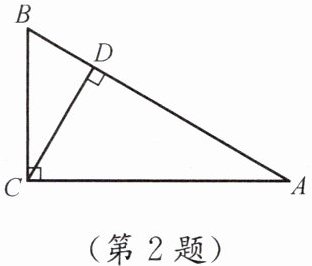
2. 如图,在 Rt△ABC 中,∠ACB = 90°,∠A = 30°,CD⊥AB,垂足为 D. △BCD 与△ABC 的周长之比为(
A.$1:2$
B.$1:3$
C.$1:4$
D.$1:5$
A
).
A.$1:2$
B.$1:3$
C.$1:4$
D.$1:5$
答案:A
3. 如图,在▱ABCD 中,CD = 10,F 是边 AB 上一点,DF 交 AC 于点 E,且$\frac{AE}{EC}=\frac{2}{5}$,则$\frac{S_{△AFF}}{S_{△CDE}}=$

$\frac{4}{25}$
,BF =6
.
答案:$\frac {4}{25}$
6
6
4. 利用复印机的缩放功能,将原图中边长为 5 cm 的一个等边三角形放大成边长为 20 cm 的等边三角形,放大前后的两个三角形的面积比为
1:16
.答案:1:16
5. 五边形 ABCDE 与五边形 A′B′C′D′E′相似,相似比为$3:2$.
(1) 如果五边形 ABCDE 的周长为 72 cm,求五边形 A′B′C′D′E′的周长;
(2) 如果五边形 A′B′C′D′E′的面积为$120 cm^2$,求五边形 ABCDE 的面积.
(1) 如果五边形 ABCDE 的周长为 72 cm,求五边形 A′B′C′D′E′的周长;
(2) 如果五边形 A′B′C′D′E′的面积为$120 cm^2$,求五边形 ABCDE 的面积.
答案:1:16
解:(1)周长之比等于相似比
∴$C_{五边形ABCDE}$:$C_{五边形A'B'C'D'E'}=3$:2
∵五边形$ABCDE = 72\ \mathrm {cm}$
∴$C_{五边形A'BC'D'E'} = 48\ \mathrm {cm}$
(2)面积之比等于相似比的平方
∴S _{五边形ABCDE}:$S_{ 五边形A'B'C'D'E'}=9$:4
∵$S_{ 五边形A'B'C'D'E' }= 120\ \mathrm {cm}²$
∴$S _{五边形ABCDE} = 270\ \mathrm {cm}²$
解:(1)周长之比等于相似比
∴$C_{五边形ABCDE}$:$C_{五边形A'B'C'D'E'}=3$:2
∵五边形$ABCDE = 72\ \mathrm {cm}$
∴$C_{五边形A'BC'D'E'} = 48\ \mathrm {cm}$
(2)面积之比等于相似比的平方
∴S _{五边形ABCDE}:$S_{ 五边形A'B'C'D'E'}=9$:4
∵$S_{ 五边形A'B'C'D'E' }= 120\ \mathrm {cm}²$
∴$S _{五边形ABCDE} = 270\ \mathrm {cm}²$
1. 如图,点 A₁、A₂,点 B₁、B₂,点 C₁、C₂ 分别是△ABC 的边 BC、CA、AB 的三等分点,若△ABC 的周长为$l$,求六边形 A₁A₂B₁B₂C₁C₂ 的周长.


答案:解:∵点${A}_1、$${A}_2,$点${B}_1、$${B}_2,$
点${C}_1、$${C}_2$分别是△ABC的边BC、CA、 AB的三等分点
∴$\frac {B{C}_2}{AB}=\frac {B{A}_1}{BC}=\frac {1}{3}$
∵∠B=∠B
∴$△B{C}_2{A}_1∽△BAC$
同理可得:$△A{B}_2{C}_1∽△ACB、$$△C{B}_1{A}_2∽△ CAB,$且相似比均为1 : 3
∴${A}_1{C}_2={B}_1{B}_2=\frac {1}{3}AC$
${A}_2{B}_1={C}_1{C}_2=\frac {1}{3}AB$
${C}_1{B}_2={A}_1{A}_2=\frac {1}{3}BC$
∴${C}_{六边形}=\frac {2}{3}{C}_{△ABC}=\frac {2}{3}l$
点${C}_1、$${C}_2$分别是△ABC的边BC、CA、 AB的三等分点
∴$\frac {B{C}_2}{AB}=\frac {B{A}_1}{BC}=\frac {1}{3}$
∵∠B=∠B
∴$△B{C}_2{A}_1∽△BAC$
同理可得:$△A{B}_2{C}_1∽△ACB、$$△C{B}_1{A}_2∽△ CAB,$且相似比均为1 : 3
∴${A}_1{C}_2={B}_1{B}_2=\frac {1}{3}AC$
${A}_2{B}_1={C}_1{C}_2=\frac {1}{3}AB$
${C}_1{B}_2={A}_1{A}_2=\frac {1}{3}BC$
∴${C}_{六边形}=\frac {2}{3}{C}_{△ABC}=\frac {2}{3}l$
2. 如图,已知△ABC 的面积为 1,分别取 AC、BC 的中点 A₁、B₁,则四边形 A₁ABB₁ 的面积为$\frac{3}{4}$,再分别取 A₁C、B₁C 的中点 A₂、B₂,取 A₂C、B₂C 的中点 A₃、B₃……依次取下去. 利用所给图形,计算$\frac{3}{4}+\frac{3}{4^2}+\frac{3}{4^3}+·s+\frac{3}{4^n}$.


答案:解:由题意可知,An,Bn是AC、BC中最靠近点C的${2}^{n}$等分点
则${S}_{四边形AnABBn}=\frac {3}{4}+\frac {3}{4²}+\frac {3}{4³}+···+\frac {3}{{4}^{n}}$
∵An,Bn是AC、BC中最靠近点C的${2}^{n}$等分点
∴△ABC∽△AnBnC,相似比为${2}^{n}$:1
∴$S_{△ABC} $:$ S_{△AnBnC}={4}^{n}$:1
∴$S_{△AnBnC} =\frac {1}{{4}^{n}}S_{△ABC} $
又∵$S_{四边形AnABB}= S_{△ABC}- S_{△AnBnC}$
∴$S_{四边形AnABBn}=1-\frac {1}{{4}^{n}}$
∴$\frac {3}{4}+\frac {3}{4²}+\frac {3}{4³}+···+\frac {3}{{4}^{n}}=1-\frac {1}{{4}^{n}}$
则${S}_{四边形AnABBn}=\frac {3}{4}+\frac {3}{4²}+\frac {3}{4³}+···+\frac {3}{{4}^{n}}$
∵An,Bn是AC、BC中最靠近点C的${2}^{n}$等分点
∴△ABC∽△AnBnC,相似比为${2}^{n}$:1
∴$S_{△ABC} $:$ S_{△AnBnC}={4}^{n}$:1
∴$S_{△AnBnC} =\frac {1}{{4}^{n}}S_{△ABC} $
又∵$S_{四边形AnABB}= S_{△ABC}- S_{△AnBnC}$
∴$S_{四边形AnABBn}=1-\frac {1}{{4}^{n}}$
∴$\frac {3}{4}+\frac {3}{4²}+\frac {3}{4³}+···+\frac {3}{{4}^{n}}=1-\frac {1}{{4}^{n}}$