1. 如图,$\sin A$等于(

A.$2$
B.$\frac{\sqrt{5}}{5}$
C.$\frac{1}{2}$
D.$\sqrt{5}$
C
).
A.$2$
B.$\frac{\sqrt{5}}{5}$
C.$\frac{1}{2}$
D.$\sqrt{5}$
答案:C
2. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$BC = 2$,$\cos B=\frac{2}{3}$,则$AB$的长是(
A.$\sqrt{5}$
B.$3$
C.$\frac{4}{5}$
D.$\sqrt{13}$
B
).A.$\sqrt{5}$
B.$3$
C.$\frac{4}{5}$
D.$\sqrt{13}$
答案:B
3. 一架$5\ m$长的梯子斜靠在墙上,测得它与地面的夹角是$65^{\circ}$,则该梯子顶端到地面的距离为(
A.$5\sin 65^{\circ}\ m$
B.$5\cos 65^{\circ}\ m$
C.$\frac{5}{\tan 65^{\circ}}\ m$
D.$\frac{5}{\cos 65^{\circ}}\ m$
A
).A.$5\sin 65^{\circ}\ m$
B.$5\cos 65^{\circ}\ m$
C.$\frac{5}{\tan 65^{\circ}}\ m$
D.$\frac{5}{\cos 65^{\circ}}\ m$
答案:A
4. 比较大小(用“>”“<”或“=”号填空).
(1)$\sin 20^{\circ}$
(2)$\cos 40^{\circ}$
(1)$\sin 20^{\circ}$
<
$\sin 30^{\circ}$;(2)$\cos 40^{\circ}$
>
$\cos 60^{\circ}$.答案:<
>
>
5. 用计算器求下列正弦值或余弦值(精确到$0.01$):
(1)$\sin 27^{\circ}=$
(2)$\cos 63^{\circ}=$
(3)$\sin 51^{\circ}25'12''=$
(4)$\cos 32.1^{\circ}=$
(1)$\sin 27^{\circ}=$
0.45
;(2)$\cos 63^{\circ}=$
0.45
;(3)$\sin 51^{\circ}25'12''=$
0.78
;(4)$\cos 32.1^{\circ}=$
0.85
.答案:0.45
0.45
0.78
0.85
0.45
0.78
0.85
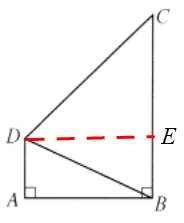
6. 如图,在四边形$ABCD$中,$\angle A=\angle ABC = 90^{\circ}$,$DB$平分$\angle ADC.$若$AD = 1$,$CD = 3$,求$\angle ABD$的正弦.

答案:
解:过点D作DE⊥BC,垂足为E
∵ ∠A=∠ABC=90°
∴ AD//BC
∴ ∠ADB=∠CBD
∵ DB平分∠ADC
∴ ∠ADB=∠CDB
∴ ∠CDB=∠CBD
∴ CD=BC=3
∵ AD=BE=1
∴ CE=BC-BE=2
在Rt△CDE中,$DE=\sqrt 5,$$BD=\sqrt{6}$
∴$ sin ∠ABD=\frac {AD}{BD}=\frac {\sqrt{6}}{6}$
解:过点D作DE⊥BC,垂足为E
∵ ∠A=∠ABC=90°
∴ AD//BC
∴ ∠ADB=∠CBD
∵ DB平分∠ADC
∴ ∠ADB=∠CDB
∴ ∠CDB=∠CBD
∴ CD=BC=3
∵ AD=BE=1
∴ CE=BC-BE=2
在Rt△CDE中,$DE=\sqrt 5,$$BD=\sqrt{6}$
∴$ sin ∠ABD=\frac {AD}{BD}=\frac {\sqrt{6}}{6}$

1. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\tan A=\frac{1}{3}$,则$\sin B=$
$\frac{3}{10}\sqrt{10}$
.答案:$\frac {3}{10}\sqrt {10}$
2. 如图,$\odot O$是$\triangle ABC$的外接圆,$AD$是$\odot O$的直径,$\odot O$的半径为$\frac{3}{2}$,$AC = 2$,则$\sin B$的值是(

A.$\frac{\sqrt{5}}{2}$
B.$\frac{\sqrt{5}}{3}$
C.$\frac{3}{2}$
D.$\frac{2}{3}$
D
).
A.$\frac{\sqrt{5}}{2}$
B.$\frac{\sqrt{5}}{3}$
C.$\frac{3}{2}$
D.$\frac{2}{3}$
答案:D
3. 等腰三角形周长为$20$,一边长为$6$,求底角的余弦.
答案:
解:作等腰三角形ABC,过顶点A作AD⊥BC,交BC于点D
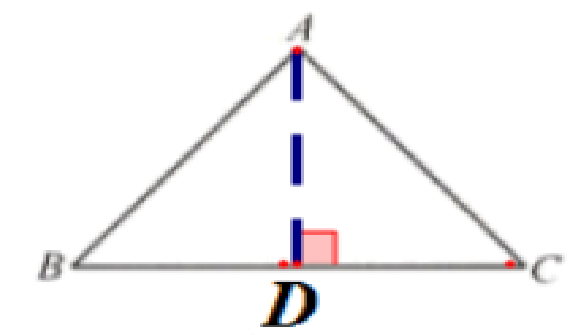
①当腰长为6时,即下图AB=6
∵$C_{△ABC}= 20$
∴BC=8
∴$BD=\frac {1}{2}BC= 4$
$cos B =\frac {BD}{AB}=\frac {2}{3}$
②当底边长为6时,即图中BC=6
∵$C_{△ABC}= 20$
∴AB=7
∴$BD=\frac {1}{2}BC= 3$
$cos B=\frac {BD}{AB}=\frac {3}{7}$
综上所述,底角的余弦为$\frac {2}{3}$或$\frac {3}{7}$
解:作等腰三角形ABC,过顶点A作AD⊥BC,交BC于点D

①当腰长为6时,即下图AB=6
∵$C_{△ABC}= 20$
∴BC=8
∴$BD=\frac {1}{2}BC= 4$
$cos B =\frac {BD}{AB}=\frac {2}{3}$
②当底边长为6时,即图中BC=6
∵$C_{△ABC}= 20$
∴AB=7
∴$BD=\frac {1}{2}BC= 3$
$cos B=\frac {BD}{AB}=\frac {3}{7}$
综上所述,底角的余弦为$\frac {2}{3}$或$\frac {3}{7}$