活动一:探究思考
阅读课本中的例3,思考下列问题.
(1) 对于一个一般的三角形,需要知道“三边”和“三角”中的几个元素才能确定这个三角形?
(2) 在$\triangle ABC$中,能直接求出$AB$吗?为什么?如果不能,你有求$AB$的办法吗?
(3) 能否通过作边$BC$(或边$AC$)上的高构造直角三角形来解决该问题?为什么?
阅读课本中的例3,思考下列问题.
(1) 对于一个一般的三角形,需要知道“三边”和“三角”中的几个元素才能确定这个三角形?
(2) 在$\triangle ABC$中,能直接求出$AB$吗?为什么?如果不能,你有求$AB$的办法吗?
(3) 能否通过作边$BC$(或边$AC$)上的高构造直角三角形来解决该问题?为什么?
答案:解:已知2个元素,其中至少有一个是边
解:不能直接求出AB,因为△ABC不是直角三角形
解:不能,因为分别构造了不可解的直角三角形。
解:不能直接求出AB,因为△ABC不是直角三角形
解:不能,因为分别构造了不可解的直角三角形。
活动二:变式思考
问题:一副三角尺按如图7 - 8所示放置,点$C$在$FD$的延长线上,$AB // CF$,$\angle F = \angle ACB = 90^{\circ}$,$\angle E = 30^{\circ}$,$\angle A = 45^{\circ}$,$AC = 12\sqrt{2}$.求$CD$的长.
(1) 线段$CD$在哪一个三角形中?关于该三角形有哪些已知条件?
(2) 请尝试构造直角三角形解决该问题.

问题:一副三角尺按如图7 - 8所示放置,点$C$在$FD$的延长线上,$AB // CF$,$\angle F = \angle ACB = 90^{\circ}$,$\angle E = 30^{\circ}$,$\angle A = 45^{\circ}$,$AC = 12\sqrt{2}$.求$CD$的长.
(1) 线段$CD$在哪一个三角形中?关于该三角形有哪些已知条件?
(2) 请尝试构造直角三角形解决该问题.

答案:
解:线段CD在△BCD中
已知BC和∠DCB=45°
解:(2)过点B作BH⊥CF 于点H
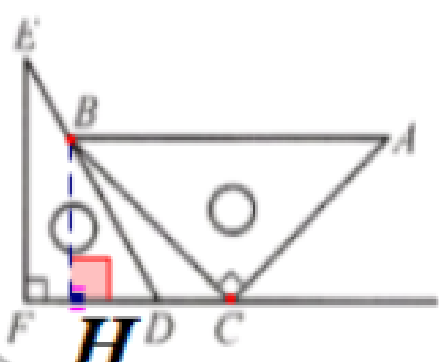
∵AB//CF
∴∠HCB=∠CBA=45°
∵∠A=45°
∴$BC= AC= 12\sqrt{2}$
∴CH=cos 45°×BC= 12
∴BH=CH= 12
∵∠E=30°
∴∠BDH= 60°
∴$DH=\frac {BH}{tan 60°}=4\sqrt{3}$
∴$CD= CH- DH = 12- 4\sqrt{3}$
解:线段CD在△BCD中
已知BC和∠DCB=45°
解:(2)过点B作BH⊥CF 于点H

∵AB//CF
∴∠HCB=∠CBA=45°
∵∠A=45°
∴$BC= AC= 12\sqrt{2}$
∴CH=cos 45°×BC= 12
∴BH=CH= 12
∵∠E=30°
∴∠BDH= 60°
∴$DH=\frac {BH}{tan 60°}=4\sqrt{3}$
∴$CD= CH- DH = 12- 4\sqrt{3}$
1. 如图,为了加快隧道开凿的施工进度,要在小山的两端同时施工.在$AC$上找一点$B$,取$\angle ABD = 145^{\circ}$,$BD = 500\ m$,$\angle D = 55^{\circ}$,如果要使点$A$、$C$、$E$成一条直线,那么开挖点$E$与点$D$的距离是(

A.$500\sin 55^{\circ}\ m$
B.$500\cos 55^{\circ}\ m$
C.$500\tan 55^{\circ}\ m$
D.$\frac{500}{\cos 55^{\circ}}\ m$
B
).
A.$500\sin 55^{\circ}\ m$
B.$500\cos 55^{\circ}\ m$
C.$500\tan 55^{\circ}\ m$
D.$\frac{500}{\cos 55^{\circ}}\ m$
答案:B